Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Nếu AB > CD thì HB > KD
⇒ HB2 > KD2
Mà : OH2 + HB2 = OK2 + KD2
⇒ OH2 < OK2
⇒ OH < OK
b) Nếu OH < OK thì OH2 < OK2
⇒ HB2 > KD2 ⇒ HB > KD
⇒ AB > CD

OH là một phần đường kính vuông góc với dây AB
⇒ H là trung điểm của AB ⇒ AB = 2HB
OK là một phần đường kính vuông góc với dây CD
⇒ K là trung điểm của CD ⇒ CD = 2KD
Theo mục 1: OH2 + HB2= OK2+ KD2
a) Ta có: AB = CD ⇒ HB = KD
⇒ OH2 = OK2 ⇒ OH = OK
b) Ta có: OH = OK ⇒ HB2 = KD2
⇒ HB = KD ⇒ AB = CD

OH là một phần đường kính vuông góc với dây AB
⇒ H là trung điểm của AB ⇒ AB = 2HB
OK là một phần đường kính vuông góc với dây CD
⇒ K là trung điểm của CD ⇒ CD = 2KD
Theo mục 1: OH2 + HB2= OK2+ KD2
Ta có: AB = CD ⇒ HB = KD
⇒ OH2 = OK2 ⇒ OH = OK

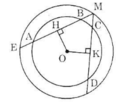
a) Trong đường tròn nhỏ:
AB > CD => OH < OK (định lí 3)
b) Trong đường tròn lớn:
OH < OK => ME > MF (định lí 3)
c) Trong đường tròn lớn:
ME > MF => MH > MK
a) Xét trong đường tròn nhỏ:
Theo định lí 22: trong hai dây của một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.
Theo giả thiết AB>CDAB>CD suy ra ABAB gần tâm hơn, tức là OH<OKOH<OK.
b) Xét trong đường tròn lớn:
Theo định lí 22: trong hai dây của một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn.
Theo câu aa, ta có: OH<OK⇒ME>MFOH<OK⇒ME>MF.
c) Xét trong đường tròn lớn:
Vì OH⊥ME⇒EH=MH=ME2OH⊥ME⇒EH=MH=ME2 (Định lý 2 - trang 103).
Vì OK⊥MF⇒KF=MK=MF2OK⊥MF⇒KF=MK=MF2 (Định lý 2 - trang 103).
Theo câu bb, ta có: ME>MF⇒ME2>MF2⇔MH>MK

Ta có \(\widehat{A}>\widehat{B}>\widehat{C}\) nên \(BC>AC>AB\)
Do đó \(OH< OI< OK\)
Nếu AB > CD thì HB > KD
⇒ HB2 > KD2
Mà : OH2 + HB2 = OK2 + KD2
⇒ OH2 < OK2
⇒ OH < OK