Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

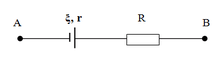
\(R_D=\dfrac{U^2_{dm}}{P_{dm}}=6\left(\Omega\right)\Rightarrow I=I_D=\dfrac{\xi}{r+R+R_D}=\dfrac{18}{1+2+6}=2\left(A\right)\)

Áp dụng định luật Ôm cho toàn mạch: E + e t c = (R + r)i
Vì r = 0 nên ta có E - L. ∆ i/ ∆ t
Từ đó suy ra tốc độ biến thiên cường độ dòng điện trong mạch:
Khi i = I 0 = 0:
![]()

Áp dụng định luật Ôm cho toàn mạch: E + e t c = (R + r)i
Vì r = 0 nên ta có E - L. ∆ i/ ∆ t
Từ đó suy ra tốc độ biến thiên cường độ dòng điện trong mạch:
Khi i = I= 2A:
![]()

\(R_1ntR_2\Rightarrow R_N=R_1+R_2=5,5+6=11,5\Omega\)
a)Cường độ dòng điện trong mạch:
\(I=\dfrac{\xi}{R_N+r}=\dfrac{12}{0,5+11,5}=1A\)
b)Hiệu điện thế: \(U=IR=1\cdot11,5=11,5V\)

Đáp án: B
HD Giải: 1 , 2 = E R 1 + 4 1 = E R 1 + 2 + 4 ⇔ 1 , 2 1 = R 1 + 6 R 1 + 4 ⇔ R 1 = 6 Ω

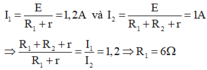
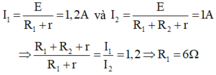
Cường độ dòng điện chạy qua đoạn mạch gồm các điện trở mắc nối tiếp luôn bằng nhau.