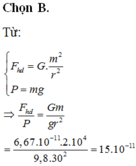Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lực hấp dẫn: \(F=G.\dfrac{m_1.m_2}{d^2}=G.\dfrac{m^2}{d^2}=6,67.10^{-11}.\dfrac{(2.10^4)^2}{40^2}=0.000016675(N)\)
Trọng lượng: \(P=mg=2.10^4.9,8=19,6.10^4(N)\)
Tỉ số: \(\dfrac{F}{P}=85.10^{-12}\)
Chọn D

Lực hấp dẫn giữa hai xe là :
Trọng lượng mỗi xe:P = mg = 196000 N

theo định luật II niu tơn
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\)
chiếu lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
F-\(\mu.m.g=m.a\) (theo phương Oy thì N=P=m.g)
\(\Rightarrow a=\)1m/s2
A.


Khi pit tông đứng yên (trước và sau khi di chuyển) nến áp suất của khí hai bên pti tông là như nhau.
Áp dụng phương trình trạng thái cho khí trong mỗi phần xilanh :
- Phần khí bị nung nóng : $\dfrac{p_0V_0}{T_0}=\dfrac{p_1V_1}{T_1} (1) $
- Phần khí bị làm lạnh : $\dfrac{p_0V_0}{T_0}=\dfrac{p_2V_2}{T_2} (2) $
Từ phương trình $(1),(2)$ và $p_1=p_2\Rightarrow \dfrac{V_1}{T_1}=\dfrac{V_2}{T_2} $
Gọi x là khoảng pit tông dịch chuyển ta có :$\dfrac{(l_0+x)S}{T_1}=\dfrac{(l_0-x)S}{T_2}\Rightarrow x=\dfrac{l_0(T_1-T_2)}{T_1+T_2} $
Thay số ta được $x=2cm$

Hướng dẫn giải:
Gọi mA là khối lượng của xe ca.
mB là khối lượng của xe móc.
Chọn trục Ox nằm ngang, chiều dương là chiều chuyển động.
Định luật II Niu-tơn cho:
a) Hợp lực tác dụng lên xe A chính là hợp lục tác dụng lên hệ (A và B).
Fhl = (mA+mB)a = (1250 +325). 2,15
=> Fhl = 3386,25 N
b) Hợp lực tác dụng lên xe B.
Fhl = mB.a
Fhl = 325. 2,15 = 698,75 N.


2)
Chọn chiều dương là chiều chuyển động. Trọng lượng của xe P=mg =1500.10=150000 N chiếu lên trục Oy ta có \(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{0}=m.a_y=0\Rightarrow P=N\) Ap luc của xe lên đường ray: N=P=150000N Lực ma sát trượt: Fmst=\(N.\mu=15000.0,45=6750\left(N\right)\) 3) Chọn chiều dương là chiều chuyển động. Trọng lượng của xe P=mg Ap luc của xe lên đường ray: N=P=m.g Từ khi hãm phanh xe chỉ chịu tác dụng của lực ma sát trượt nên theo định luật II Niutơn, gia tốc của xe là: a=\(-\dfrac{F_{ms}}{m}=-\dfrac{\mu.m.g}{m}=-\mu.g\)=−0,2.9,8=−1,96m/s^2 Gọi s là đường đi từ khi hãm phanh đến lúc dừng lại. \(S=\dfrac{v^2-v_0^2}{2a}=\dfrac{0-\left(\dfrac{36}{3,6}\right)^2}{2.\left(-1,96\right)}\approx25,5\left(m\right)\)