Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
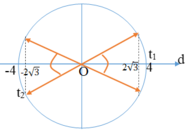
Khoảng cách giữa hai vật theo phương Ox là:
![]()
Theo bài ra ta có d ≥ 2√3
Trong khoảng t1 = 1/24 s đến t2 = 1/3s = t1 + T/2 +T/12, d có độ lớn không nhỏ hơn 2√3 trong khoảng thời gian là:
∆t = T/12 + 2. T/12 = 1/8s.

Đáp án B
+ Khoảng cách giữa hai dao động được biểu diễn bằng một hàm điều hòa
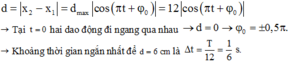

Phương trình khoảng cách giữa 2 vật :
\(\Delta x=10\cos\left(\pi t\right)cm\)
Tại thời điểm 2 vật đi ngang qua nhau tức là cùng li độ.
Thời gian ngắn nhất chúng cách nhau thỏa mãn tại thời điểm t1, chúng cùng đi qua VTCB (tốc độ cực đại)
Thời gian \(\Delta x\)từ 0 đến 5cm xác định trên đường tròn
\(t=\frac{T}{12}=\frac{1}{6}s\)
Chọn A

\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

Chọn đáp án C
+ Theo đề: x = x 1 − x 2 = 10 3 cos 4 π t + φ c m
+ Giả sử chọn t = 0 ⇒ x = x 0 = 10 3 c m nghĩa là t 1 : x = 10 3 cos 4 π t 1 = ± 15 ⇔ cos 4 π t 1 = ± 3 2
Tại t 1 : x = 10 3 cos 4 π t 1 = ± 15 ⇔ cos 4 π t 1 = ± 3 2
⇒ 4 π t 1 = π 6 ⇒ t 1 = 1 24 s (Từ biên A đến vị trí A 3 2 )
+ Theo hình vẽ ở tai thời điểm t1: 4 π t 1 = π 6 ⇒ t 1 = 1 24 s
Theo hình vẽ dễ thấy 2 thời điểm gần nhất là 2 lần t1
Từ M1 đến M2: t 2 − t 1 = 2 t 1 = 2 24 = 1 12 s t

Mỗi câu hỏi bạn nên hỏi 1 bài thôi để tiện trao đổi nhé.
Biểu diễn dao động bằng véc tơ quay ta có:
M x 2 1 O N
Để vật qua li độ 1 cm theo chiều dương thì véc tơ quay qua N.
Trong giây đầu tiên, véc tơ quay đã quay 1 góc là: \(5\pi\), ứng với 2,5 vòng quay.
Xuất phát từ M ta thấy véc tơ quay quay đc 2,5 vòng thì nó qua N 3 lần do vậy trong giây đầu tiên, vật qua li độ 1cm theo chiều dương 3 lần.
Bạn xem thêm lí thuyết phần này ở đây nhé
Phương pháp véc tơ quay và ứng dụng | Học trực tuyến
Bài 1 :
T = 2π / ω = 0.4 s
Vật thực hiện được 2 chu kì và chuyển động thêm trong 0.2 s (T/2 ) nữa
1 chu kì vật qua vị trí có li độ x=2cm theo chiều dương được "1 " lần
⇒ 2 ________________________________________... lần
phần lẻ 0.2s (T/2) , (góc quét là π ) (tức là chất điểm CĐ tròn đều đến vị trí ban đầu và góc bán kính quét thêm π (rad) nữa, vị trí lúc nầy:
x = 1 + 2cos(-π/2 + π ) = 1, (vận tốc dương) vật qua vị trí có li độ x=2cm theo chiều dương thêm 1 lần nữa
(từ VT ban đầu (vị tri +1 cm ) –> biên dương , về vị trí có ly độ x = +1 cm
do đó trong giây đầu tiên kể từ lúc t=0 vật qua vị trí có li độ x=2cm theo chiều dương được 3 lần
Chọn A

Ta có $x_1=x_{12}-x_2=x_{12}-(x_{23}-(x_{13}-x_1)$
$\Rightarrow$ $2x_1=x_{12}-x_{23}+x_{13}$. Bấm máy tính ta được
${x_1}={3\sqrt{6}}\cos\left({\pi t + \dfrac{\pi}{12}} \right)$
${x_3}={3\sqrt{2}}\cos\left({\pi t + \dfrac{7\pi}{12}} \right)$
Suy ra hai dao động vuông pha, như vậy khi x1 đạt giá trị cực đại thì x3 bằng 0.
![]()
cách bấm máy để ra phương trình dao động làm như thế nào vậy ạ

Chọn đáp án C
Theo đề: x = x 1 − x 2 = 10 3 cos 4 π t + φ c m
Giả sử chọn φ = 0 nghĩa là t = 0 ⇒ x = x 0 = 10 3 c m
Tại t 1 : x = 10 3 cos 4 π t 1 = ± 15 ⇔ cos 4 π t 1 = ± 3 2
⇒ 4 π t 1 = π 6 ⇒ t 1 = 1 24 s (Từ biên A đến vị trí A 3 2 )
Theo hình vẽ ở tai thời điểm t 1 : 4 π t 1 = π 6 ⇒ t 1 = 1 24 s
Theo hình vẽ dễ thấy 2 thời điểm gần nhất là 2 lần t 1
Từ M 1 đ ế n M 2 : t 2 − t 1 = 2 t 1 = 2 24 = 1 12 s t
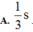
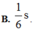
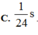
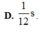
Biểu diễn hai dao động bởi 2 vecto quay chung gốc, có độ dài khác nhau.
Pha ban đầu của hai dao động tạo với nhau goc 900 và không thay đổi khi hai vật chuyển động (do hai vật chuyển động cùng tốc độ góc).
Ta có:
Khi khoảng cách giữa hai vật là 6 cm thì góc tạo bởi MN với Ox là :
Ta có: thì gian ngắn nhất để khoảng cách giữa hai vật là 6cm chính là thời gian để vecto quay được góc 900 – 600 = 300.
Nên
Đáp án D