Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình khoảng cách giữa 2 vật :
\(\Delta x=10\cos\left(\pi t\right)cm\)
Tại thời điểm 2 vật đi ngang qua nhau tức là cùng li độ.
Thời gian ngắn nhất chúng cách nhau thỏa mãn tại thời điểm t1, chúng cùng đi qua VTCB (tốc độ cực đại)
Thời gian \(\Delta x\)từ 0 đến 5cm xác định trên đường tròn
\(t=\frac{T}{12}=\frac{1}{6}s\)
Chọn A

Chọn A
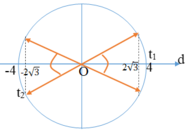
Khoảng cách giữa hai vật theo phương Ox là:
![]()
Theo bài ra ta có d ≥ 2√3
Trong khoảng t1 = 1/24 s đến t2 = 1/3s = t1 + T/2 +T/12, d có độ lớn không nhỏ hơn 2√3 trong khoảng thời gian là:
∆t = T/12 + 2. T/12 = 1/8s.

x=Acos(\(\omega t+\varphi\))
Tại thời điểm t=0, ta có:
\(\frac{A}{2}=Acos\left(\varphi\right)\) \(\Rightarrow\)\(\varphi=-\frac{\pi}{6}\)(do vật chuyển động theo chiều dương)
\(\Rightarrow\) \(x=Acos\left(\omega t-\frac{\pi}{6}\right)\)
cái này mình tưởng phải bằng: x=Acos(\(\omega t+\frac{\pi}{3}\)) chứ.

Đáp án A
+ Biểu diễn hai vị trí tương ứng trên đường tròn, ta dễ dàng xác định được △ φ = 0 , 5 π
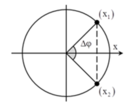

Chọn đáp án C
+ Theo đề: x = x 1 − x 2 = 10 3 cos 4 π t + φ c m
+ Giả sử chọn t = 0 ⇒ x = x 0 = 10 3 c m nghĩa là t 1 : x = 10 3 cos 4 π t 1 = ± 15 ⇔ cos 4 π t 1 = ± 3 2
Tại t 1 : x = 10 3 cos 4 π t 1 = ± 15 ⇔ cos 4 π t 1 = ± 3 2
⇒ 4 π t 1 = π 6 ⇒ t 1 = 1 24 s (Từ biên A đến vị trí A 3 2 )
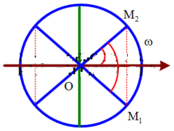
+ Theo hình vẽ ở tai thời điểm t1: 4 π t 1 = π 6 ⇒ t 1 = 1 24 s
Theo hình vẽ dễ thấy 2 thời điểm gần nhất là 2 lần t1
Từ M1 đến M2: t 2 − t 1 = 2 t 1 = 2 24 = 1 12 s t

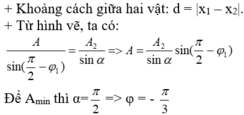
Đáp án A
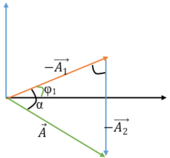
Giả sử tại thời điểm ban đầu hai chất điểm đều có tọa độ là x = 6 cm và ngược chiều nhau
φ 1 = 53 0 φ 2 = - 45 0