

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn đáp án D
Ta có: λ = 3 c m
Vì M 1 , M 2 cùng nằm trên elip nhận A,B làm tiêu điểm
⇒ A M 1 + B M 1 = A M 2 + B M 2
Phương trình dao động của điểm M là
u M 1 = 2 A cos π AM 1 - BM 1 λ cos 10 π t - π ( A M 1 - B M 1 ) λ ⇒ u M 1 = 4 cos 10 πt + ϕ u M 2 = 2 A cos π ( AM 2 - BM 2 λ cos 10 π t - π A M 2 - B M 2 λ ⇒ u M 2 = - 4 3 cos 10 π t + ϕ t ạ i t h ờ i đ ể m t t h ì u M 1 = 3 ⇒ cos ( 10 π t + ϕ ) = 0 , 75 t h a y v à o p h ư ơ n g t r ì n h u M 2 ⇒ u M 2 = - 3 3 m m

Bước sóng: \(\lambda=\frac{15}{5}=3cm\)
\(AM_1-BM_1=\frac{\lambda}{3}\)
\(AM_2-BM_2=\lambda+\frac{\lambda}{6}\)
Như vậy, M1 và M2 nằm trên sườn của 2 gợn lồi liên tiếp nên M1 dao động ngược pha với M2
Biên độ M1: 4cm.
Biên độ M2: \(4\sqrt{3}cm\)
Ta có: \(\frac{u_1}{u_2}=-\frac{A_1}{A_2}\Leftrightarrow\frac{3}{u_2}=-\frac{4}{4\sqrt{3}}\Leftrightarrow u_2=-3\sqrt{3}cm\)
@Tuấn: Bạn cứ liên tưởng đến hiện tượng như sóng dừng ấy: Các điểm thuộc cùng một bó sóng dao động cùng pha, 2 điểm thuộc 2 bó liên tiếp dao động ngược pha.
Trong giao thoa sóng, các điểm dao động cực đại tương đương như bụng sóng của hiện tượng sóng dừng.
Hai điểm cực đại liên tiếp coi như thuộc 2 bó sóng liên tiếp.
Trong giao thoa sóng thì:
\(-\frac{\lambda}{2}\le d_2-d_1\le\frac{\lambda}{2}\) thuộc bó trung tâm (chứa đường trung trung của AB)
\(\frac{\lambda}{2}\le d_2-d_1\le\frac{3\lambda}{2}\)thuộc bó thứ 1
\(\frac{3\lambda}{2}\le d_2-d_1\le\frac{5\lambda}{2}\)thuộc bó thứ 2
.....
Theo hiệu khoảng cách d2 - d1 trong đề bài thì M1, M2 có thể coi thuộc 2 bó liên tiếp nên nó dao động ngược pha.

Đáp án C
Phương pháp:
Phương trình giao thoa sóng tại một điểm trong vùng giao thoa 2 nguồn cùng biên độ a là:
![]()
Cách giải:
Phương trình sóng tại điểm:
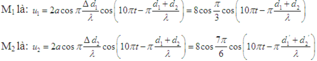
Do hai điểm M1 và M2 cùng nằm trên một elip nhận A, B làm tiêu điểm nên có:
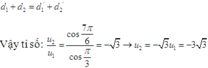

Đáp án D
Ta có bước sóng λ = v f = 3(cm)
Mọi điểm nằm trên Elip có tiêu điểm là A và B đều có cùng pha dao động.
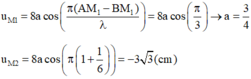

\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

Chọn đáp án B
+ Bước sóng: λ = v f = 6 c m
+ Phương trình sóng tổng hợp tại một điểm: u = 2 a c o s π d 1 − d 2 λ c o s 10 π t − π d 1 + d 2 λ
+Vì d 1 + d 2 = A B ⇒ u M u N = c o s π d 2 M − d 1 M λ c o s π d 1 N − d 2 N λ = c o s 2 π 6 c o s 6 π 6 = − 1 2 ⇒ 2 u N = − 1 2 ⇒ u N = − 2 2 m m

Đáp án D
Hai nguồn giống nhau, có λ = 3 c m nên phương trình sóng tại M 1 và M 2 là:
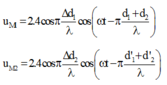
Mà
M
1
và
M
2
nằm trên cùng một elip nên ta luôn có ![]()
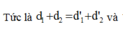
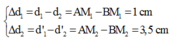
Nên ta có tỉ số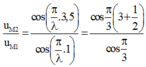
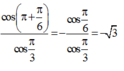
![]()