Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ - A B C q1 q2 E1 E2 E
Nhận xét: Do \(AB^2=AC^2+BC^2\) nên tam giác ABC vuông tại C.
Điện trường tổng hợp tại C là: \(\vec{E}=\vec{E_1}+\vec{E_2}\)
Suy ra độ lớn: \(E=\sqrt{E_1^2+E_2^2}\) (*) (do \(\vec{E_1}\) vuông góc với \(\vec{E_2}\) )
\(E_1=9.10^9.\dfrac{16.10^{-8}}{0,04^2}=9.10^5(V/m)\)
\(E_1=9.10^9.\dfrac{9.10^{-8}}{0,03^2}=9.10^5(V/m)\)
Thay vào (*) ta được \(E=9\sqrt2.10^5(V/m)\)

Đáp án: C
Để cường độ điện trường tại M bằng 0 thì hai vecto E 1 do q1 gây ra và E 2 do q2 gây ra phải ngược chiều và cùng độ lớn nên M nằm trên đường thẳng AB và ngoài đoạn AB
Do |q2| > |q1| nên r1 < r2 => r1 = r2 - AB,
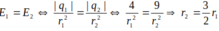
=>![]()

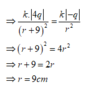
Chọn đáp án B
Hai điện tích q 1 , q 2 trái dấu nên điểm có cường độ điện trường tổng hợp bằng 0 phải nằm ngoài đoạn thẳng AB và do q 1 , q 2 nên điểm này phải nằm về phía B.
Ta biểu diễn cường độ điện trường tại C như trên hình.