Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)
Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)
Giải thích: Đáp án A
Phương pháp: Sử dụng lí thuyết về lực kéo về trong dao động điều hòa của con lắc lò xo kết hợp với kĩ năng đọc đồ thị
Cách giải:
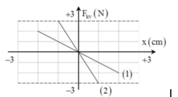
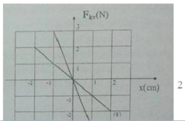
- Từ đồ thị ta thu được các dữ kiện sau:
CLLX1 có biên độ dao động A1 = 2cm, lực kéo về cực đại F1max = 2 N
=> Độ cứng của lò xo 1 là k1 = 100 N/m
CLLX2 có biên độ dao động A2 = 1 cm, lực kéo về cực đại F2max = 3 N
=> Độ cứng của lò xo 2 là k2 = 300 N/m
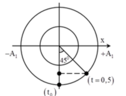
- Theo đề bài, tại thời điểm ban đầu, cả hai con lắc đều đi qua VTCB theo một chiều, ở đây giả sử theo chiều dương.
+ Sau thời gian ngắn nhất t = 0,5 thì CLLX1 qua vị trí có động năng bằng nửa cơ năng, tức là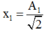 
=> thời gian t = T1/8 => T1 = 4t = 4 s
Và động năng khi đó của con lắc là: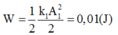 
+ Ta có: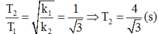 
=> Sau thời gian t = 0,5s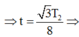 
Khi đó CLLX 2 đang ở vị trí có li độ x2 = 0,98 cm
=> Thế năng của con lắc 2 là: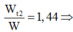 
Chọn A
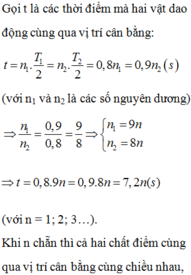
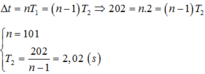
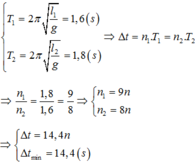
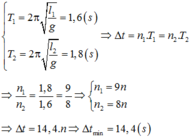
+ Sau khoảng thời gian Δt, con lắc 1 thực hiện được n1 dao động và con lắc 2 thực hiện được n2 dao động:
Δ t = n 1 T 1 = n 2 T 2 ⇒ n 1 n 2 = T 2 T 1 = 0 , 85 1 , 13 = 85 113 ⇒ n 1 = 85 n n 2 = 113 n
⇒ Δ t = 85 n T 1 = 96 , 05 n s ⇒ Δ t min = 96 , 05 s
Chọn đáp án B