Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vận tốc cực đại của electron bắn ra từ catode là \(v\). Ta có:
\(\frac{mv^2}{2}=eU_h\) (\(U_h=2V\) là hiệu điện thế hãm)
\(\Rightarrow v=\sqrt{\frac{2U_he}{m}}=8,4.10^5\text{(m/s)}\)
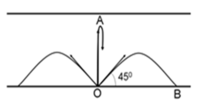
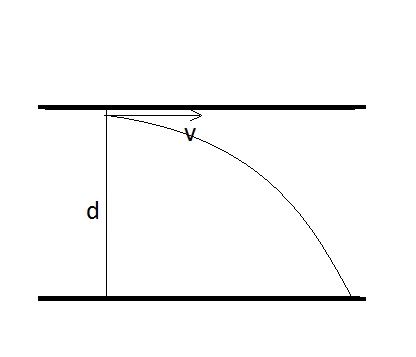
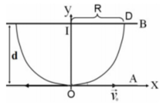
Vận tốc này có thế theo mọi hướng, để đập vào anode với bán kính lớn nhất thì electron sẽ có vận tốc theo phương song song với bản phẳng.
|
\(t=\sqrt{\frac{2d}{a}}=\sqrt{\frac{2d^2m_e}{U_e}}=2,4.10^{-8}\left(s\right)\)
Bán kính lớn nhất:
\(r=vt=0,02\left(m\right)=2\left(cm\right)\)
\(chọn.A\)

Ta có
Wđ= \(\frac{hc}{\lambda}\)
lấy tỉ lệ
1,5=\(\frac{hc}{1.2\lambda}\) => \(\lambda\)
sau đó A=\(\frac{hc}{\lambda}\)
không biết có đúng không. Nếu sai sót mong mn góp ý ạ![]()

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Hệ thức Anh -xtanh trong hiện tượng quang điện
\(hf = A_1+W_{đ1}.(1)\)
\(hf = A_2+W_{đ2}.(2)\)
Ta có \(A_1 = \frac{hc}{\lambda_{01}}; A_2 = \frac{hc}{\lambda_{02}}\)
\( \lambda_{02} = 2\lambda_{01}=> A_1 = 2A_2. \)
Trừ vế với vế của phương trình (1) cho phương trình (2) ta có
=> \(0= A_1-A_2+W_{đ 1}-W_{đ 2}.\)
=> \(W_{đ2}=( A_1-A_2)+W_{đ1} = A_2+W_{đ1}\)
Mà \(A_2 >0\) => \(W_{đ2} > W_{đ1}\).
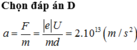
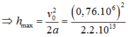
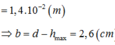
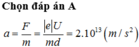
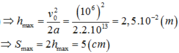
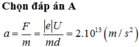
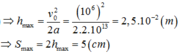
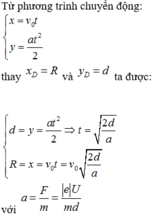
Đáp án: D
UBA = 4,55V nên chiều điện trường từ B sang A, do vậy e chịu lực cản của lực điện trường chiều từ A sang B.
Ta có:
a = F/m = |e|U/md = 2.1013 m/s2
=> hmax = vo2/2a = (0,76.106)2 / (2.2.1013)=1,4.10-2 m
=>Các electron quang điện có thể tới cách bản B một đoạn gần nhất là:
s = d - hmax = 2,6cm