Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có:
\(f\left(x_1\right)=ax_1+b=0\)
\(f\left(x_2\right)=ax_2+b=0\)
\(\Rightarrow f\left(x_1\right)-f\left(x_2\right)=0-0\)
\(\Rightarrow a\left(x_1-x_2\right)=0\)
\(x_1\ne x_2\Rightarrow x_1-x_2\ne0\)
\(\Rightarrow a=0\)
\(\Rightarrow f\left(x_1\right)=0=0+b\Rightarrow b=0\)
Như vậy với mọi giá trị của x thì đa thức trên luôn bằng 0.
Vậy f(x) là đa thức 0.

Phương trình tiếp tuyến tại M0 có dạng: y = k(x – x0) + y0 (*)
Với x0 là hoành độ tiếp điểm;
Với y0 = f(x0) là tung độ tiếp điểm;
Với k = y’(x0) = f’(x0) là hệ số góc của tiếp tuyến.
Để viết được phương trình tiếp tuyến ta phải xác định được x0; y0 và k

x1+x2+x3+...+x51=0
(x1+x2)+(x3+x4)+...+(x49+x50)+x51=0
1+1+...+1+x51=0 (25 số 1)
x51=0-25
x51=-25

ta có x1+x2=1;x3+x4=1;...;x49+x50=1
mà x1+x2+x3+...+x50+x51=0
hay (x1+x2)+(x3+x4)+...+(x49+x50)+x51=0
1+1+1+1+..+1+x51=0(có 25 thừa số 1)
1*25+x51=0
25+x51=0
x51=0-25
x51=-25

Theo hệ thức Vi-et ta có:
\(x_1+x_2=\frac{2\left(m-1\right)}{m+2}=\frac{2m+4}{m+2}-\frac{6}{m+2}=2-\frac{6}{m+2}\Rightarrow m+2=\frac{-6}{x_1+x_2-2}\)
\(x_1.x_2=\frac{3-m}{m+2}=\frac{-m-2}{m+2}+\frac{5}{m+2}=-1+\frac{5}{m+2}\Rightarrow m+2=\frac{5}{x_1.x_2+1}\)
Suy ra: \(-\frac{6}{x_1+x_2-2}=\frac{5}{x_1.x_2+1}\)<=>-6x1.x2-6=5x1+5x2-10 <=>5x1+5x2+6x1.x2-4 (pt cần tìm)
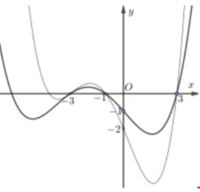
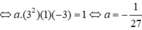
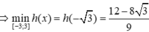




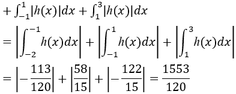


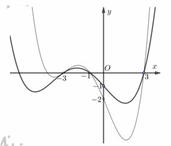
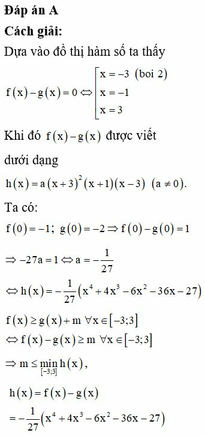
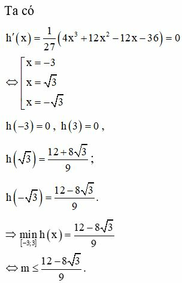
Chọn đáp án C
Hoành độ giao điểm của đồ thị hai hàm số f(x) và g(x) là nghiệm của phương trình
Từ giả thiết, ta có x1, x2, x3 là ba nghiệm của phương trình (1).
Theo định lý Viets thì x 1 + x 2 + x 3 = 3
Mặt khác ta có
Suy ra