Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
![]() .
.
Vì ![]() nên phương trình
nên phương trình ![]() có 2 nghiệm phân biệt.
có 2 nghiệm phân biệt.
Do đó hàm số có hai điểm cực trị ![]() .
.
Giả sử hàm số có hai điểm cực trị lần lượt là ![]() và
và ![]() , với
, với ![]() ,
, ![]() là nghiệm của phương trình
là nghiệm của phương trình ![]() .
.
Thực hiện phép chia ![]() cho
cho ![]() ta được :
ta được : ![]() .
.
Khi đó ta có: 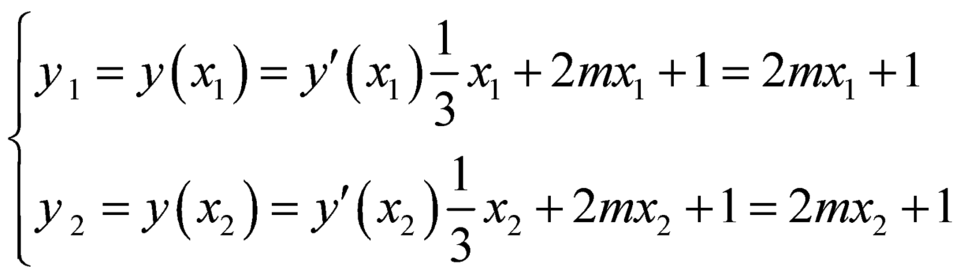 .
.
Ta thấy, toạ độ hai điểm ![]() và
và ![]() thoả mãn phương trình
thoả mãn phương trình ![]() .
.
Do đó, phương trình đường thẳng qua hai điểm cực trị là ![]() .
.
Ta thấy ![]() luôn qua
luôn qua ![]() .
.
Đặt ![]()
![]() .
.
![]() .
.
Xét hàm số ![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
Suy ra hàm số ![]() liên tục và đồng biến trên
liên tục và đồng biến trên ![]() .
.
Do đó ![]() .
.
Vậy ![]() đạt giá trị lớn nhất
đạt giá trị lớn nhất ![]()
![]() .
.

Đạo hàm y’ = 3x2 – 3m
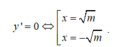
Hàm số có 2 cực trị khi và chỉ khi : m> 0
Khi đó tọa độ 2 điểm cực trị của đồ thị hàm số là:
M ( m ; - 2 m m + 2 ) N ( - m ; 2 m m + 2 ) ⇒ M N → = ( - 2 m ; 4 m m )
Phương trình đường thẳng MN: 2mx+ y-2=0
Ta có :
S ∆ I A B = 1 2 I A . I B . sin A I B ^ = 1 2 sin A I B ^ ≤ 1 2
Dấu bằng xảy ra khi
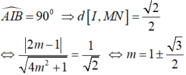
Chọn B.

Chọn B
[Phương pháp tự luận]
y ' = 3 x 2 - 3 m
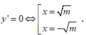
Hàm số có 2 cực trị khi và chỉ khi m > 0
Khi đó tọa độ 2 điểm cực trị của đồ thị hàm số là : M ( m ; - 2 m m + 2 )
![]()
Phương trình đt MN : 2 m x + y - 2 = 0
![]()
![]()
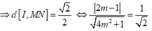
⇔ m = 1 ± 3 2

Đáp án A
+ Phương trình hoành độ giao điểm: ![]()
+ Điều kiện để d cắt tại hai điểm phân biệt là ![]() .
.
+ Trung điểm của MN là I.
+ Theo công thức đường trung tuyến 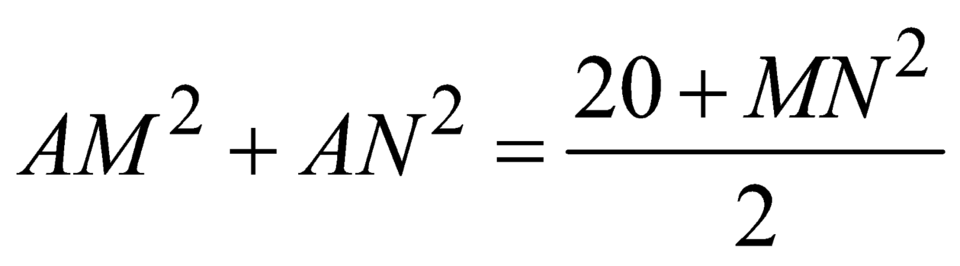 .
.
![]() nhỏ nhất khi
nhỏ nhất khi ![]() nhỏ nhất.
nhỏ nhất.
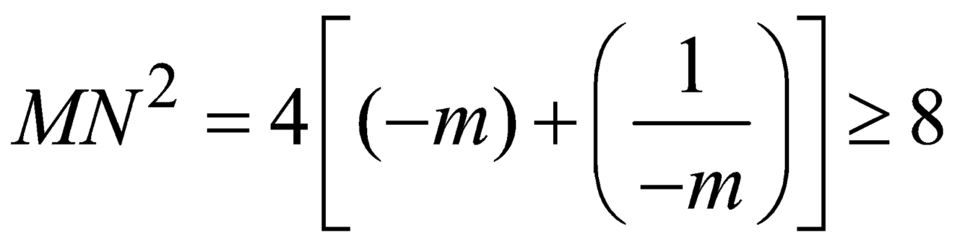 , dấu bằng xảy ra khi
, dấu bằng xảy ra khi ![]()

Chọn D
Phương trình hoành độ giao điểm :
![]()
Theo yêu cầu bài toán : ![]() phải có hai nghiệm phân biệt khác
phải có hai nghiệm phân biệt khác ![]()
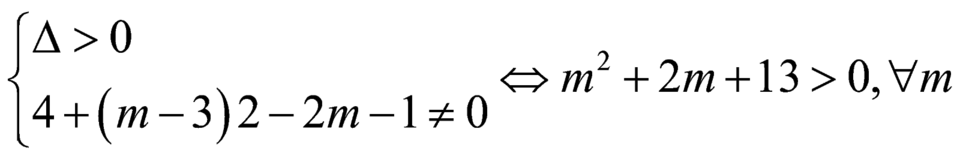
Gọi ![]() ,
,![]() suy ra
suy ra ![]() là trọng tâm của tam giác
là trọng tâm của tam giác ![]() :
:
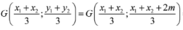
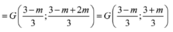
Theo yêu cầu bài toán :
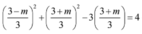
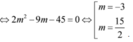 .
.

Phương trình hoành độ giao điểm
x3+2mx2+3(m-1)x+2 =-x+2 hay x(x2+2mx+3(m-1))=0
suy ra x=0 hoặc x2+2mx+3(m-1)=0 (1)
Đường thẳng d cắt (C) tại ba điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác 0
⇔ m 2 - 3 m + 3 > 0 m - 1 ≠ 0 ⇔ ∀ m m ≠ 1 ⇔ m ≠ 1
Khi đó ta có: C( x1 ; -x1+2) ; B(x2 ; -x2+2) trong đó x1 ; x2 là nghiệm của (1) ; nên theo Viet thì x 1 + x 2 = - 2 m x 1 x 2 = 3 m - 3
Vậy
C B → = ( x 2 - x 1 ; - x 2 + x 1 ) ⇒ C B = 2 ( x 2 - x 1 ) 2 = 8 ( m 2 - 3 m + 3 )
d ( M ; ( d ) ) = - 3 - 1 + 2 2 = 2
Diện tích tam giác MBC bằng khi và chỉ khi
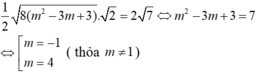
Chọn B.

a) Hàm có cực đại, cực tiểu khi mà $y'=-3x^2+2(m-1)x=x[2(m-1)-3x]$ có ít nhất hai nghiệm phân biệt $\Leftrightarrow 2(m-1)-3x=0$ có một nghiệm khác $0$ hay $m\neq 1$
b) Đồ thị hàm số $(\star)$ cắt trục hoành tại ba điểm phân biệt khi mà phương trình $y=-x^3+(m-1)x^2-m+2=0$ có $3$ nghiệm phân biệt
$\Leftrightarrow (1-x)[x^2+x(2-m)+(2-m)]=0$ có ba nghiệm phân biệt
$\Leftrightarrow x^2+x(2-m)+(2-m)=0$ có hai nghiệm phân biệt khác $1$
Do đó ta cần có $\left\{\begin{matrix}1+2-m+2-m=5-2m\neq 0\\ \Delta =(2-m)^2-4(2-m)>0\end{matrix}\right.$
Vậy để thỏa mãn đề bài thì $m\neq \frac{5}{2}$ và $m>2$ hoặc $m<-2$
c) Gọi điểm cố định mà đồ thị hàm số đi qua là $(x_0,y_0)$
$y_0=-x_0^3+(m-1)x_0^2-m+2$ $\forall m\in\mathbb{R}$
$\Leftrightarrow m(x_0^2-1)-(x_0^3+x_0^2+y_0-2)=0$ $\forall m\in\mathbb{R}$
$\Rightarrow\left{\begin{matrix}x_0^2=1\\ x_0^3+x_0^2+y_02=0\end{matrix}\right.\begin{bmatrix}(x_0,y_0)=(1;0)\\ (x_0,y_0)=(-1;2)\end{bmatrix}$
Viết lại đoạn cuối:
$\Rightarrow\left{\begin{matrix}x_0^2=1\\x_0^3+x_0^2+y_0-2=0\end{matrix}\right.$ $\Rightarrow \begin{bmatrix}(x_0,y_0)=(1;0)\\ (x_0,y_0)=(-1;2)\end{bmatrix}$

Chọn C