Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k ⇒ A’B’= kAB
M’ = F(M) ⇒ A’M’ = kAM
M là trung điểm AB ⇒ AM = 1/2 AB ⇒ kAM = 1/2 kAB hay A’M’= 1/2 A’B’
Vậy M’ là trung điểm của A’B’

a) Gọi H là trung điểm của BC
△ABC có: E là trung điểm của AC, H là trung điểm của BC
Suy ra: EH // AB
Mà AB // A'B'
Do đó: EH // A'B' hay EH // B'F (1)
Ta có: EH // AB nên \(\dfrac{EH}{AB}=\dfrac{EC}{AC}=\dfrac{1}{2}\)
Mà AB = A'B', B'F = \(\dfrac{1}{2}\) A'B'
Nên: EH = B'F (2)
(1)(2) suy ra: EHB'F là hình bình hành. Do đó: EF // B'H
Mà B'H thuộc (BCC'B')
Suy ra: EF // (BCC'B')
b) Gọi K là trung điểm AB
Dễ dàng chứng minh được FKBB' là hình bình hành
Ta có: FK // BB'
Mà BB' // CC'
Suy ra: FK // CC' (1)
Ta có: FK = BB', mà BB' = CC'
Do đó: FK = CC' (2)
(1)(2) suy ra FKCC' là hình bình hành
Mà hai đường chéo của hình bình hành cắt nhau tại trung điểm mỗi đường
Nên C'K cắt CF tại trung điểm của hai đường thẳng
mà C'K thuộc (AC'B) , CF cắt (AC'B) tại I (đề bài)
Do đó: I là trung điểm của CF.

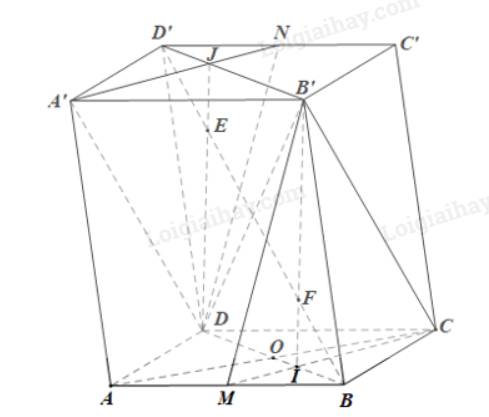
a)
Ta có: (ADD’A’) // (CBC’B’);
(ADD’A’) ∩ (DCB’A’) = A’D;
(CBC’B’) ∩ (DCB’A’) = B’C.
Do đó A’D // B’C, mà B’C ⊂ (B’CM) nên A’D // (B’CM).
Tương tự: (ABB’A’) // (DCC’D’);
(ABB’A’) ∩ (DMB’N) = MB’;
(DCC’D’) ∩ (DMB’N) = DN.
Do đó MB’ // DN, mà MB’ ⊂ (B’CM) nên DN // (B’CM).
Ta có: A’D // (B’CM);
DN // (B’CM);
A’D, DN cắt nhau tại điểm D và cùng nằm trong mp(A’DN)
Do đó (A’DN) // (B’CM).
b)
Trong mp(A’B’C’D’), gọi J là giao điểm của A’N và B’D’.
Trong mp(BDD’B’), D’B cắt DJ tại E.
Ta có: D’B ∩ DJ = {E} mà DJ ⊂ (A’DN) nên E là giao điểm của D’B và (A’DN).
Tương tự, trong mp(ABCD), gọi I là giao điểm của CM và BD.
Trong mp(BDD’B’), D’B cắt B’I tại F.
Ta có: D’B ∩ B’I = {F} mà B’I ⊂ (B’CM) nên F là giao điểm của D’B và (B’CM).
• Ta có: (A’DN) // (B’CM);
(A’DN) ∩ (BDD’B’) = DJ;
(B’CM) ∩ (BDD’B’) = B’I.
Do đó DJ // B’I.
Trong mp(BDD’B’), xét DBDE có IF // DE nên theo định lí Thalès ta có: \(\frac{{BI}}{{BD}} = \frac{{BF}}{{BE}}\) (1)
Trong mp(ABCD), gọi O là giao điểm của hai đường chéo AC và BD trong hình bình hành ABCD. Khi đó O là trung điểm của AC, BD.
Xét ∆ABC, hai đường trung tuyến BO, CM cắt nhau tại I nên I là trọng tâm của tam giác
Suy ra \(\frac{{BI}}{{BO}} = \frac{2}{3}\) hay \(\frac{{BI}}{{\frac{1}{2}BD}} = \frac{{2BI}}{{BD}} = \frac{2}{3}\)
Do đó \(\frac{{BI}}{{BD}} = \frac{1}{3}\) (2)
Từ (1) và (2) suy ra \(\frac{{BF}}{{BE}} = \frac{1}{3}\)
Suy ra \(\frac{{D'E}}{{D'F - D'E}} = \frac{1}{{3 - 1}}\) hay \(\frac{{D'E}}{{EF}} = \frac{1}{2}\).
Chứng minh tương tự ta cũng có \(\frac{{D'E}}{{D'F}} = \frac{{D'J}}{{D'B'}} = \frac{1}{3}\)
Suy ra \(\frac{{D'E}}{{D'F - D'E}} = \frac{1}{{3 - 1}}\) hay \(\frac{{D'E}}{{EF}} = \frac{1}{2}\)
Do đó \(\frac{{BF}}{{EF}} = \frac{{D'E}}{{EF}} = \frac{1}{2}\) nên BF = D’E = ½ EF.

a) Gọi M' (x₁' ; y₁' ), N' (x₂' ; y₂ )
* M' là ảnh của M qua phép F, nên toạ độ M' thoả:
{x₁' = x₁.cosα – y₁.sinα + a
{y₁' = x₁.sinα + y₁.cosα + b
* N' là ảnh của N qua phép F, nên toạ độ N' thoả:
{x₂' = x₂.cosα – y₂.sinα + a
{y₂' = x₂.sinα + y₂.cosα + b
b) * Khoảng cách d giữa M và N là:
d = MN = √ [(x₂ - x₁)² + (y₂ - y₁)²]
* Khoảng cách d' giữa M' và N' là:
d' = M'N' = √ [(x₂' - x₁' )² + (y₂' - y₁' )²]
= √ {[x₂.cosα – y₂.sinα + a - (x₁.cosα – y₁.sinα + a)]² + [x₂.sinα + y₂.cosα + b - (x₁.sinα + y₁.cosα + b)]²}
= √ {[cosα(x₂ - x₁) - sinα(y₂ - y₁)]² + [sinα(x₂ - x₁) + cosα(y₂ - y₁)]²}
= √ [(x₂ - x₁)².(cos²α + sin²α) + (y₂ - y₁)².(cos²α + sin²α)]
= √ [(x₂ - x₁)² + (y₂ - y₁)²]
c) Phép F là phép dời hình vì: MN = M'N' = √ [(x₂ - x₁)² + (y₂ - y₁)²]
d) Khi α = 0 ⇒ cosα = 1, sinα = 0
Suy ra:
{x' = x + a
{y' = y + b
Đây là biểu thức toạ độ của phép tịnh tiến. Vậy F là phép tịnh tiến

Cho tứ diện ABCD . Gọi G1,G2,G3 lần lượt là trọng tâm của các tam giác ABC,ACD,ABD . Chứng minh mặt phẳng (G1G2G3) // (BCD)

Đáp án D
Phát biểuđúng: a , c, e, f, g, i, j, l
b. Phép biến hình biến đường tròn thành đường tròn có bán kính bằng nó có thể là phép tịnh tiến
d. Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính
h. Với bất kì 2 điểm A, B và ảnh A’, B’ của chúng qua 1 phép dời hình, ta luôn có AB = A’B’.
k. Nếu phép dời hình biến điểm A thành điểm B thì nó cũng biến điểm B thành A (phát biểu không đúng với phép tịnh tiến)

a: Xét ΔSAD có
M,N lần lượt là trung điểm của SA,SD
=>MN là đường trung bình của ΔSAD
=>MN//AD
Ta có: MN//AD
AD\(\subset\)(ABCD)
MN không nằm trong mp(ABCD)
Do đó: MN//(ABCD)
b: Xét ΔDSB có
O,N lần lượt là trung điểm của DB,DS
=>ON là đường trung bình của ΔDSB
=>ON//SB và \(ON=\dfrac{SB}{2}\)
Ta có: ON//SB
ON\(\subset\)(OMN)
SB không thuộc mp(OMN)
Do đó: SB//(OMN)
c: Xét ΔASC có
O,M lần lượt là trung điểm của AC,AS
=>OM là đường trung bình của ΔASC
=>OM//SC
Ta có: OM//SC
OM\(\subset\)(OMN)
SC không nằm trong mp(OMN)
Do đó: SC//(OMN)
Ta có: SB//(OMN)
SC//(OMN)
SB,SC cùng thuộc mp(SBC)
Do đó: (SBC)//(OMN)
Gọi A', B', M' lần lượt là ảnh của A, B, M qua phép dời hình F
Theo tính chất 1 ⇒ AB = A'B' và AM = A'M' (1)
M là trung điểm AB ⇒ AM = 1/2 AB
Kết hợp (1) ⇒ A'M' = 1/2 A'B' ⇒ M' là trung điểm A'B'