
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


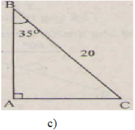
∠B = 90o - ∠C = 90o - 35o = 55o
b = asinB = 20.sin35o ≈ 11,47 (cm)
c = asinC = 20.sin55o ≈ 16,38 (cm)

a: \(\widehat{B}=45^0\)
\(b=c=10cm\)
\(a=\sqrt{2\cdot b^2}=10\sqrt{2}\left(cm\right)\)
b: \(\widehat{C}=90^0-35^0=55^0\)
\(b=a\cdot\sin B=11,47\left(cm\right)\)
\(c=\sqrt{a^2-b^2}=16,38\left(cm\right)\)

a) (H.a)
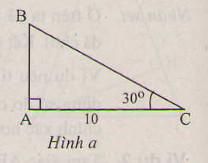
ˆB=90∘−30∘=60∘.B^=90∘−30∘=60∘.
AB=AC⋅tgC=10⋅tg30∘≈5,774(cm)AB=AC⋅tgC=10⋅tg30∘≈5,774(cm)
BC=ACcosC=10cos30∘≈11,547(cm)BC=ACcosC=10cos30∘≈11,547(cm).
b) (H.b)
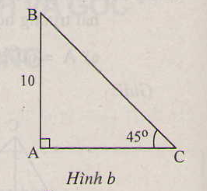
ˆB=90∘−45∘=45∘.B^=90∘−45∘=45∘.
⇒AC=AB=10(cm);⇒AC=AB=10(cm);
BC=ABsinC=10sin45∘≈14,142(cm)BC=ABsinC=10sin45∘≈14,142(cm)
c) (H.c)
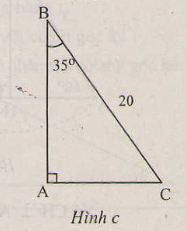
ˆC=90∘−35

Ta có: \(\widehat{CAH}=\widehat{B}\left(=90^0-\widehat{C}\right)\)
mà \(\widehat{B}=60^0\)
nên \(\widehat{CAH}=60^0\)
Xét ΔAHC vuông tại H có
\(HC=AC\cdot\sin\widehat{CAH}\)
\(\Leftrightarrow AC=\dfrac{20}{\dfrac{\sqrt{3}}{2}}=\dfrac{40\sqrt{3}}{3}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(BC=AC:\dfrac{\sqrt{3}}{2}\)
\(=\dfrac{40\sqrt{3}}{3}\cdot\dfrac{2}{\sqrt{3}}=\dfrac{80}{3}\left(cm\right)\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+BC+CA\)
\(=\dfrac{40\sqrt{3}}{3}+\dfrac{40}{3}+\dfrac{80}{3}\)
\(=\dfrac{120+40\sqrt{3}}{3}\)

I là tâm đường tròn nội tiếp tam giác và E là tiếp điểm
nên IE⊥AC, mà A^=90o suy ra IE//AB
⇒ANEI=AMEM
⇒AN=AM.EIEM=AC.EI2(AM−AE) (1)
Tứ giác AEIF là hình vuông nên AE=EI;
D, E, F là các tiếp điểm
⇒AE+CD+BD=12(BC+CA+AB)⇒AE=AC+AB−BC2,
thay vào (1) ta được ...

bán kính đường tròn ngoại tiếp tam giác vuông bằng nửa cạnh huyền
=>BC=10
AC=6
AB=8
chu vi ABC=10+6+8=24

Câu hỏi của Trần Dần - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo nhé!
∠B = 90o - ∠C = 90o - 35o = 55o
b = asinB = 20.sin35o ≈ 11,47 (cm)
c = asinC = 20.sin55o ≈ 16,38 (cm)