Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Cách chia 9 đội ra thành 3 bảng là: C 9 3 C 6 3 C 3 3 = 1680
Cách chia 3 đội bóng của Việt Nam ở 3 bảng khác nhau là C 3 1 C 6 2 C 2 1 C 4 2 = 540
=> p = 540 1680 = 9 28

Đáp án A.
Không gian mẫu là số cách chia tùy ý 12 đội thành 3 bảng.
Suy ra số phần tử của không gian mẫu là n Ω = C 12 4 . C 8 4 . C 4 4 .
Gọi X là biến cố “3 đội bóng của Việt Nam ở 3 bảng khác nhau”
Bước 1: Xếp 3 đội Việt Nam ở 3 bảng khác nhau nên có 3! cách.
Bước 2: Xếp 6 đội còn lại vào 3 bảng A, B, C này có C 9 3 . C 6 3 . C 3 3 .
Suy ra số phần tử của biến cố X là n X = 3 ! . C 9 3 . C 6 3 . C 3 3 .
Vậy xác suất cần tính là P = n X n Ω = 3 ! . C 9 3 . C 6 3 . C 3 3 C 12 4 . C 8 4 . C 4 4 = 16 55 .

Đáp án A.
Không gian mẫu là số cách chia tùy ý 12 đội thành 3 bảng.
Suy ra số phần tử của không gian mẫu là n Ω = C 12 4 . C 8 4 . C 4 4 .
Gọi X là biến cố “3 đội bóng của Việt Nam ở 3 bảng khác nhau”
Bước 1: Xếp 3 đội Việt Nam ở 3 bảng khác nhau nên có 3! cách.
Bước 2: Xếp 6 đội còn lại vào 3 bảng A, B, C này có C 9 3 . C 6 3 . C 3 3 .
Suy ra số phần tử của biến cố X là n X = 3 ! . C 9 3 . C 6 3 . C 3 3 .
Vậy xác suất cần tính là P = n X n Ω = 3 ! . C 9 3 . C 6 3 . C 3 3 C 12 4 . C 8 4 . C 4 4 = 16 55 .

Đáp án B
Số cách sắp ngẫu nhiên là C 9 3 C 6 3 C 3 3 = 1680 (cách)
Số cách sắp để ba đội của Việt Nam ở 3 bảng khác nhau là: C 6 2 C 3 1 C 4 2 C 2 1 C 2 2 C 1 2 = 540 (cách)
Xác suất để 3 đội bóng của Việt Nam ở 3 bảng khác nhau là: 540 1680 = 9 28

Chọn D
Chia 8 đội bóng thành 2 bảng đấu có ![]()
Gọi A là biến cố: “Hai đội Việt Nam nằm ở hai bảng đấu khác nhau”


Số cách chia 8 đội thành 2 bảng là:
![]()
Gọi A là biến cố: “Hai đội của Việt Nam được xếp vào 2 bảng khác nhau”.
Số các chia 2 đội của Việt Nam vào 2 đội là:
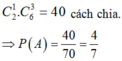
Chọn D.

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m


Đáp án C
Cách chia 9 đội ra thành 3 bảng là:
C 9 3 C 6 3 C 3 3 = 1680
Cách chia 3 đội bóng của Việt Nam ở 3 bảng khác nhau là: C 3 1 C 6 2 C 2 1 C 4 2 = 540
⇒ p = 540 1680 = 9 28