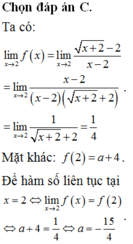
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
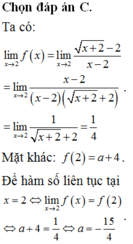
Đơn giản là bạn vẽ cái hàm bậc 4 đó ra và cho -m và -m-10 cắt thôi. Vì -m-10<-m nên -m-10 sẽ nằm ở dưới, còn -m nằm trên. Nên -m sẽ cắt 2 điểm và -m-10 cắt 4 điểm cho ta 6 điểm. Ngoài ra k còn trường hợp nào khác mà -m và -m-10 cắt thỏa mãn
Chọn A
Hàm số y = f(x) = 2 x + m x - 1 . xác định và liên tục trên [2;3].
Với m = -2, hàm số trở thành y = 2
(không thỏa)
Với 
ta có: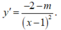 
Khi đó hàm số luôn đồng biến hoặc nghịch biến trên [2;3]
Suy ra 
Do đó: 
Theo giả thiết 
Vậy tổng các giá trị của tham số thỏa mãn yêu cầu bài toán là: -4.
Nhận xét: đề bài cho thêm dấu giá trị tuyệt đối ở trong biểu thức 
là không cần thiết.
Chọn A
Hàm số y = f(x) =
2
x
+
m
x
-
1
xác định và liên tục trên [2;3]
Với m = -2, hàm số trở thành y = 2 
(không thỏa).
Với m
≠
2, ta có: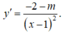 
Khi đó hàm số luôn đồng biến hoặc nghịch biến trên [2;3]
Suy ra
Do đó:
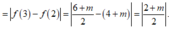
Theo giả thiết
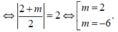
Vậy tổng các giá trị của tham số thỏa mãn yêu cầu bài toán là: -4.
Nhận xét: đề bài cho thêm dấu giá trị tuyệt đối ở trong biểu thức 
là không cần thiết.
Chọn D
Xét hàm số 
Ta có 
nên 
Vì vậy 
khi t = 2
⇔
x = 1
Mặt khác 
Suy ra 
khi x = 1
Vậy 
⇔
m = 3
Cách 2: Tác giả: Nguyễn Trọn g Lễ; Fb: Nguyễn Trọng Lễ.
Phương pháp trắc nghiệm
Chọn hàm y = f(x) = 4 thỏa mãn giả thiết: hàm số y = f(x) liên tục trên ℝ có
Ta có 
Xét hàm số g(x) liên tục trên đoạn [0;2], g'(x) = 0 ⇔ x = 1. Ta có g(0) = 4 + m, g(1) = 5 + m, g(2) = 4 + m
Rõ ràng g(0) = g(2) < g(1) nên 
Vậy 5 + m = 8 => m = 3
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x-sinx=0\\x-m-3=0\\x-\sqrt{9-m^2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=m+3\\x=\sqrt{9-m^2}\end{matrix}\right.\)
Do hệ số bậc cao nhất của x dương nên:
- Nếu \(m=-3\Rightarrow f'\left(x\right)=0\) có nghiệm bội 3 \(x=0\) \(\Rightarrow x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m=3\Rightarrow x=0\) là nghiệm bội chẵn (không phải cực trị, ktm)
- Nếu \(m=0\Rightarrow x=3\) là nghiệm bội chẵn và \(x=0\) là nghiệm bội lẻ, đồng thời \(x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m\ne0;\pm3\) , từ ĐKXĐ của m \(\Rightarrow-3< m< 3\Rightarrow\left\{{}\begin{matrix}m+3>0\\\sqrt{9-m^2}>0\end{matrix}\right.\)
Khi đó \(f'\left(x\right)=0\) có 3 nghiệm pb trong đó \(x=0\) là nghiệm nhỏ nhất
Từ BBT ta thấy \(x=0\) là cực tiểu
Vậy \(-3\le m< 3\)
cho em hỏi là tại sao m≠0 mà đkxđ của m lại là -3<m<3 ạ ?
9 đko nhỉ