Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\frac{1}{x-3}=a,\frac{1}{y-4}=b\)
\(hpt\Leftrightarrow\hept{\begin{cases}a+b=\frac{5}{3}\\4a-3b=\frac{3}{2}\end{cases}\Rightarrow\hept{\begin{cases}a=\frac{13}{14}\\b=\frac{31}{42}\end{cases}\Rightarrow}}\hept{\begin{cases}x=\frac{53}{13}\\y=\frac{166}{31}\end{cases}}\)
Đặt m = 1 / x - 3 và n = 1/y - 4
Khi đó ta có hệ m + n = 5/3
4 x x - 3 x n = 3/2
....Bạn tự giải tiếp nhé
Bài toán giải hệ phương trình bằng phương pháp thế có 2 cách trình bày.
Cách 1:
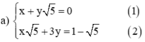
Từ (1) ta rút ra được x = -y√5 (*)
Thế (*) vào phương trình (2) ta được :
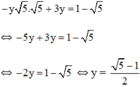
Thay y = 5 - 1 2 vào (*) ta được: x = − 5 − 1 2 ⋅ 5 = 5 − 5 2
Vậy hệ phương trình có nghiệm 5 − 5 2 ; 5 − 1 2
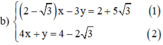
Từ (2) ta rút ra được y = -4x + 4 - 2 √3 (*)
Thế (*) vào phương trình (1) ta được:
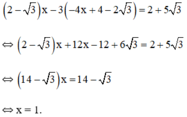
Thay x = 1 vào (*) ta được y = -4.1 + 4 - 2√3 = -2√3
Vậy hệ phương trình có nghiệm duy nhất (1; -2√3)
Cách 2 :
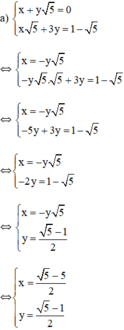
Vậy hệ phương trình có nghiệm duy nhất 5 − 5 2 ; 5 − 1 2
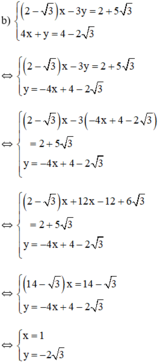
Vậy hệ phương trình có nghiệm duy nhất (1; -2√3)
Kiến thức áp dụng
Giải hệ phương trình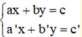 
ta làm như sau:
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
Câu dễ làm trước !
b) \(\hept{\begin{cases}x^4+x^2y^2+y^4=481\\x^2+xy+y^2=37\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(x^2+y^2\right)-x^2y^2=481\\x^2+xy+y^2=37\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(x^2-xy+y^2\right)=13\\x^2+xy+y^2=37\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}xy=12\\x^2+y^2=25\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\left(x^2+2xy+y^2\right)-xy=37\\\left(x^2-2xy+y^2\right)+xy=13\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(x+y\right)^2=49\\\left(x-y\right)^2=1\end{cases}}\) (thay xy=12)
\(\Leftrightarrow\hept{\begin{cases}x=4\\y=3\end{cases}}\) hoặc \(\hept{\begin{cases}x=-4\\y=-3\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\hept{\begin{cases}x+y=7\\x-y=1\end{cases}}\\\hept{\begin{cases}x+y=-7\\x-y=-1\end{cases}}\end{cases}}\)
\(\left\{{}\begin{matrix}\left(x-5\right)\left(y-2\right)=\left(x+2\right)\left(y-1\right)\\\left(x-4\right)\left(y+7\right)=\left(x-3\right)\left(y+4\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy-2x-5y+10=xy-x+2y-2\\xy+7x-4y-28=xy+4x-3y-12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+7y=12\\3x-y=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x+21y=36\\3x-y=16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}22y=20\\x+7y=12\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{62}{11}\\y=\dfrac{10}{11}\end{matrix}\right.\)
\(\hept{\begin{cases}x-y=3\\3x-4y=2\end{cases}}\)
\(\hept{\begin{cases}x=y+3\\3x-4y=2\end{cases}}\)
\(\hept{\begin{cases}x=y+3\\3y+9-4y=2\end{cases}}\)
\(\hept{\begin{cases}x=y+3\\y=7\end{cases}}\)
\(\hept{\begin{cases}x=10\left(tm\right)\\y=7\left(tm\right)\end{cases}}\)
Vậy (x;y)=(10;7)
\(\hept{\begin{cases}\frac{x}{2}-\frac{y}{3}=1\\5x-8y=3\end{cases}}\)
\(\hept{\begin{cases}x-\frac{2y}{3}=2\\5x-8y=3\end{cases}}\)
\(\hept{\begin{cases}x=\frac{2y}{3}+2\\10+\frac{10y}{3}-8y=3\end{cases}}\)(thay x =2y/3 + 2 vào bthuc bên cạnh )
\(\hept{\begin{cases}x=2+\frac{2}{3}y\\-\frac{14}{3}y=-7\end{cases}}\)
\(\hept{\begin{cases}x=2+\frac{2}{3}\cdot\frac{3}{2}=3\\y=\frac{3}{2}\end{cases}}\)
Vậy (x;y)=(3:3/2)
\(1,\Leftrightarrow\left\{{}\begin{matrix}x=2y+4\\-4y-8+5y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\cdot5+4=14\\y=5\end{matrix}\right.\\ 2,\Leftrightarrow\left\{{}\begin{matrix}5x-30+6x=3\\y=10-2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\\ 3,\Leftrightarrow\left\{{}\begin{matrix}x=4-2y\\6y-12+y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{10}{7}\\y=\dfrac{19}{7}\end{matrix}\right.\)
Cách 1
Từ (1) rút ra được y = x – 3
Thế vào phương trình (2) ta được:
3x – 4.(x – 3) = 2 ⇔ 3x – 4x + 12 = 2 ⇔ x = 10
Từ x = 10 ⇒ y = x – 3 = 7.
Vậy hệ phương trình có nghiệm duy nhất (10 ; 7).
Từ (2) rút ra được y = -4x + 2.
Thế y = -4x + 2 vào phương trình (1) ta được :
7x – 3.(-4x+2) = 5 ⇔ 7x + 12x – 6 = 5 ⇔ 19x = 11 ⇔ x= 11/19
Vậy hệ phương trình có nghiệm duy nhất ( 11/19;-6/19)
Từ (1) rút x theo y ta được: x = -3y – 2
Thế x = -3y – 2 vào phương trình (2) ta được :
5.(-3y – 2) – 4y = 11 ⇔ -15y – 10 – 4y = 11 ⇔ -19y = 21 ⇔ y = - 21/19
Vậy hệ phương trình có nghiệm duy nhất ( 25/19; -21/19)
Cách 2
Kiến thức áp dụng
Giải hệ phương trình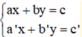
ta làm như sau:
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn)..
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương ..
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.