Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Động năng của proton: K 1 = K 2 + K 3 - ∆ E = 5 , 48 M e V
Gọi p là động lượng của của một vật; p = m v ; K = m v 2 2 = p 2 2 m
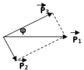
Theo định luật bảo toàn động lượng thì p 1 = p 2 + p 3
Suy ra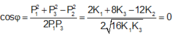 
Vậy nên φ = π 2
Đáp án B.
Động năng của proton: K1 = K2 + K3 - ∆E = 5,48 MeV
Gọi P là động lượng của một vật; P = mv; 
P12 = 2m1K1 = 2uK1; P22 = 2m2K2 = 12uK2 ; P32 = 2m3K3 = 8uK3
\(_1^1p + _4^9Be \rightarrow \alpha + _3^6Li\)
Phản ứng này thu năng lượng => \(W_{thu} =(m_s-m_t)c^2 = K_t-K_s\)
=> \( K_p+ K_{Be}-K_{He}- K_{Li} = W_{thu} \) (do Be đứng yên nên KBe = 0)
=> \(K_p = W_{thu}+K_{Li}+K_{He} = 2,125+4+3,575 = 9,7MeV.\)
Áp dụng định luật bảo toàn động lượng
P P P α α p Li
\(\overrightarrow P_{p} =\overrightarrow P_{He} + \overrightarrow P_{Li} \)
Dựa vào hình vẽ ta có
Áp dụng định lí hàm cos trong tam giác
=> \(\cos {\alpha} = \frac{P_p^2+P_{He}^2-P_{Li}^2}{2P_pP_{He}} = \frac{2.1.K_p+ 2.4.K_{He}-2.6.K_{Li}}{2.2.2m_pm_{He}K_pK_{He}} = 0.\)
Với \(P^2 = 2mK, m=A.\).
=> \(\alpha = 90^0.\)
Đáp án C:
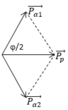
Theo ĐL bảo toàn động lượng: 
P2 = 2mK (K là động năng) nên 
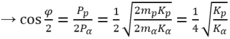
(Vì phản ứng tỏa năng lượng) 
Kp = 2Ka + ∆ E -----> KP - DE = 2Ka ------> KP > 2Ka
Do đó ta chọn đáp án C: góc j có thể 1600
