Dựa vào công thức (1) và định lý sin, hãy chứng minh S = abc/4R.

K

Khách

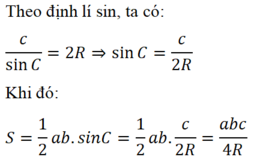
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PT

Pham Trong Bach

17 tháng 4 2017

Dựa vào công thức (1) và định lý sin, hãy chứng minh S = abc/4R.

#Toán lớp 10

1

CM

Cao Minh Tâm

17 tháng 4 2017

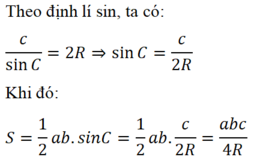
Giải bài tập Toán 10 | Giải Toán lớp 10

Các câu hỏi dưới đây có thể giống với câu hỏi trên

QT

Quoc Tran Anh Le

Giáo viên

25 tháng 9 2023

Cho tam giác ABC như Hình 10.

a) Viết công thức tính diện tích S của tam giác ABC theo a và \({h_a}\)

b) Tính \({h_a}\) theo b và sinC.

c) Dùng hai kết quả trên để chứng minh công thức \(S = \frac{1}{2}ab\sin C\)

d) Dùng định lí sin và kết quả ở câu c) để chứng minh công thức \(S = \frac{{abc}}{{4R}}\)

#Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

25 tháng 9 2023

a) Diện tích S của tam giác ABC là: \(S = \frac{1}{2}a.{h_a}\)

b) Xét tam giác vuông AHC ta có: \(\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b}\)

\( \Rightarrow {h_a} = b.\sin C\)

c) Thay \({h_a} = b.\sin C\) vào công thức diện tích, ta được: \(S = \frac{1}{2}ab\sin C\)

d) Theo định lí sin ta có: \(\frac{c}{{\sin C}} = 2R \Rightarrow \sin C = \frac{c}{{2R}}\)

Thay vào công thức ở c) ta được: \(S = \frac{1}{2}ab\frac{c}{{2R}} = \frac{{abc}}{{4R}}.\)

DT

ĐỖ THỊ THANH HẬU

4 tháng 1 2020

Cho tam giác ABC có diện tích là S và bán kính đường tròn ngoại tiếp R thỏa mãn hệ thức

\(S=\frac{2}{3}R^3\left(\sin^3A+\sin^3B+\sin^3C\right)\) Chứng minh tam giác ABC đều

#Toán lớp 10

1

PN

ミ★๖ۣۜPɦạм ๖ۣۜNɠυүệт๖ۣۜBăηɠ ★彡

5 tháng 1 2020

Sai đề hay sao ý!

SG

Sách Giáo Khoa

8 tháng 4 2017

Chứng minh rằng trong tam giác ABC ta có các hệ thức :

a) \(\sin A=\sin B\cos C+\sin C\cos B\)

b) \(h_a=2R\sin B\sin C\)

#Toán lớp 10

1

NT

Nguyen Thuy Hoa

19 tháng 5 2017

Các hệ thức lượng giác trong tam giác và giải tam giác

Các hệ thức lượng giác trong tam giác và giải tam giác

QT

Quoc Tran Anh Le

Giáo viên

24 tháng 9 2023

Cho tam giác ABC có BC = a, AC = b, AB =c và diện tích là S. (Hình 24).

a) Từ định lí cosin, chứng tỏ rằng:

\(\sin A = \frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} \) ở đó \(p = \frac{{a + b + c}}{2}\)

b) Bằng cách sử dụng công thức \(S = \frac{1}{2}bc\sin A\),hãy chứng tỏ rằng: \(S = \sqrt {p(p - a)(p - b)(p - c)} \)

#Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

24 tháng 9 2023

Áp dụng định lí cosin trong tam giác ABC ta có:

\({a^2} = {b^2} + {c^2} - 2bc.\cos A\)\( \Rightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)

Mà \(\sin A = \sqrt {1 - {{\cos }^2}A} \).

\( \Rightarrow \sin A = \sqrt {1 - {{\left( {\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}} \right)}^2}} = \sqrt {\frac{{{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}}}{{{{(2bc)}^2}}}} \)

\( \Leftrightarrow \sin A = \frac{1}{{2bc}}\sqrt {{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}} \)

Đặt \(M = \sqrt {{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}} \)

\(\begin{array}{l} \Leftrightarrow M = \sqrt {(2bc + {b^2} + {c^2} - {a^2})(2bc - {b^2} - {c^2} + {a^2})} \\ \Leftrightarrow M = \sqrt {\left[ {{{(b + c)}^2} - {a^2}} \right].\left[ {{a^2} - {{(b - c)}^2}} \right]} \\ \Leftrightarrow M = \sqrt {(b + c - a)(b + c + a)(a - b + c)(a + b - c)} \end{array}\)

Ta có: \(a + b + c = 2p\)\( \Rightarrow \left\{ \begin{array}{l}b + c - a = 2p - 2a = 2(p - a)\\a - b + c = 2p - 2b = 2(p - b)\\a + b - c = 2p - 2c = 2(p - c)\end{array} \right.\)

\(\begin{array}{l} \Leftrightarrow M = \sqrt {2(p - a).2p.2(p - b).2(p - c)} \\ \Leftrightarrow M = 4\sqrt {(p - a).p.(p - b).(p - c)} \\ \Rightarrow \sin A = \frac{1}{{2bc}}.4\sqrt {p(p - a)(p - b)(p - c)} \\ \Leftrightarrow \sin A = \frac{2}{{bc}}.\sqrt {p(p - a)(p - b)(p - c)} \end{array}\)

b) Ta có: \(S = \frac{1}{2}bc\sin A\)

Mà \(\sin A = \frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} \)

\(\begin{array}{l} \Rightarrow S = \frac{1}{2}bc.\left( {\frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} } \right)\\ \Leftrightarrow S = \sqrt {p(p - a)(p - b)(p - c)} .\end{array}\)

BT

Bình Trần Thị

16 tháng 5 2016

chứng minh nếu tam giác ABC có 3 góc A , B , C và 3 cạnh a , b , c thỏa mãn đẳng thức sau thì tam giác ABC vuông : \(\frac{b}{\cos B}\) + \(\frac{c}{\cos C}\) = \(\frac{a}{\sin B.\sin C}\)

#Toán lớp 10

0

SG

Sách Giáo Khoa

8 tháng 4 2017

Chứng minh rằng biểu thức sau đây không phụ thuộc vào \(\alpha\) :

a) \(A=\left(\sin\alpha+\cos\alpha\right)^2+\left(\sin\alpha-\cos\alpha\right)^2\)

b) \(B=\sin^4\alpha-\cos^4\alpha-2\sin^2\alpha+1\)

#Toán lớp 10

1

BT

Bùi Thị Vân

18 tháng 5 2017

a)
\(A=\left(sin\alpha+cos\alpha\right)^2+\left(sin\alpha-cos\alpha\right)^2\)
\(=1+2sin\alpha cos\alpha+1-2sin\alpha cos\alpha=2\) (không phụ thuộc vào \(\alpha\)).
b)
\(B=sin^4\alpha-cos^4\alpha-2sin^2\alpha+1\)
\(=\left(sin^2\alpha+cos^2\alpha\right)\left(sin^2\alpha-cos^2\alpha\right)-2sin^2\alpha+1\)
\(=sin^2\alpha-cos^2\alpha-2sin^2\alpha+1\)
\(=-sin^2\alpha-cos^2\alpha+1\)
\(=-\left(sin^2\alpha+cos^2\alpha\right)+1=-1+1=0\).

BT

Bình Trần Thị

18 tháng 5 2016

chứng minh nếu tam giác ABC có 3 góc A , B , C và 3 cạnh a , b , c thỏa mãn đẳng thức sau thì tam giác ABC vuông : \(\frac{b}{\cos B}\) + \(\frac{c}{\cos C}\) = \(\frac{a}{\sin B\times\sin C}\)

#Toán lớp 10

1

HT

Hồng Trinh

18 tháng 5 2016

định lý hàm số sin:
a/ \(\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=\)2R
=> a = 2R.sinA = 2R.sin[180^o - (B+C)] = 2R.sin(B+C)
và b = 2R.sinB; c = 2R.sinC thay vào (*) được:
\(\frac{2R\times sinB}{cosB}+\frac{2R\times sinC}{cosC}=\frac{2R\times sin\left(B+C\right)}{sinBsinC}\)
<=>sinB/cosB + sinC/cosC = sin(B+C)/(sinB.sinC)
<=> sin(B+C)/(cosBcosC) = sin(B+C)/(sinB.sinC)
<=> cosBcosC = sinB.sinC
<=> cosBcosC - sinB.sinC = 0
<=> cos(B+C) = 0
<=> B+C = 90^o
vậy tam giác ABC vuông tại A

BT

Bình Trần Thị

17 tháng 5 2016

Câu hỏi hay

chứng minh nếu tam giác ABC có 3 góc A , B , C và 3 cạnh a , b , c thỏa mãn đẳng thức sau thì tam giác ABC vuông : \(\frac{b}{\cos B}\) + \(\frac{c}{\cos C}\) = \(\frac{a}{\sin B\times\sin C}\)

#Toán lớp 10

1

HD

Hà Đức Thọ

Admin

18 tháng 5 2016

b/cosB+c/cosC=a/sinB.sinC (*)

Áp dụng định lý hàm số sin:
a/sinA = b/sinB = c/sinC = 2R
=> a = 2R.sinA = 2R.sin[180⁰ - (B+C)] = 2R.sin(B+C)
và b = 2R.sinB; c = 2R.sinC thay vào (*) được:
2R.sinB/cosB + 2RsinC/cosC = 2R.sin(B+C)/(sinB.sinC)
<=>sinB/cosB + sinC/cosC = sin(B+C)/(sinB.sinC)
<=> sin(B+C)/(cosBcosC) = sin(B+C)/(sinB.sinC)
<=> cosBcosC = sinB.sinC
<=> cosBcosC - sinB.sinC = 0
<=> cos(B+C) = 0
<=> B+C = 90⁰

NT

Ngô Tấn Đạt

25 tháng 8 2016

lần đầu e thấy thầy giải luôn

BT

Bình Trần Thị

17 tháng 5 2016

chứng minh nếu tam giác ABC có 3 góc A , B , C và 3 cạnh a , b , c thỏa mãn đẳng thức sau thì tam giác ABC vuông : \(\frac{b}{\cos B}\) + \(\frac{c}{\cos C}\) = \(\frac{a}{\sin B\times\sin C}\)

#Toán lớp 10

0