Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cường độ dòng hiệu dụng qua mỗi cuộn dây là \(I\)
Công suất động cơ: \(P=3.U.I\cos\varphi\Rightarrow I = \dfrac{P}{3.U\cos\varphi}=5A\)

Vecto của hiệu điện thế hai đầu mạch bằng tổng hai vecto hiệu điện thế của động cơ điện và cuộn dây
Vẽ giản đồ vecto ta có thể tổng hợp và tính độ lớn của hiệu điện thế hai đầu mạch
Dùng phép chiếu tính các giá trị theo thành phần thẳng đứng và nằm ngang
\(U_x=U\cos15+2U\cos75\)
\(U_y=U\sin15+2U\sin75\)
\(U=\sqrt{U^2_x+U^2_y}=U\sqrt{7}\)

Đáp án D


Dựa vào giản đồ xét tam giác vuông OAB có
\(\sin60=\frac{Uc}{U_{ }AB}\Rightarrow U_C=100.\sin60=50\sqrt{3}V\Rightarrow Z_C=\frac{U_C}{I}=\frac{50\sqrt{3}}{0.5}=100\sqrt{3}\Omega\)
=> \(C=\frac{1}{Z_C.\omega}\)
\(\cos60=\frac{U_R}{U_{AB}}\Rightarrow U_R=50\Omega\Rightarrow R=\frac{U_R}{I}=100\Omega\)
2. Công suất trên mạch có biểu thức
\(P=I^2R=\frac{U^2}{R^2+\left(Z_L-Z_C\right)^2}.R\\=\frac{U^2}{R^{ }+\frac{\left(Z_L-Z_C\right)^2}{R}}\)
L thay đổi để P max <=> Mẫu Min => áp dụng bất đẳng thức cô-si cho hai số không âm=> \(R=\left|Z_L-Z_C\right|\)
=> \(R=100-40=60\Omega\)
=>

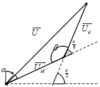
Biểu diễn vecto các điện áp. Ta có thể đơn giản hóa động cơ điện là một mạch điện đơn giản gồm cuộn cảm và điện trở trong.
→ Hiệu suất của động cơ H = A P
→ 0 , 8 = 7500 U M .40. cos 30 0 → U M = 271 V.
Áp dụng định lý cos trong tam giác ta có
→ U = U M 2 + U d 2 − 2 U M U d cos β V
Áp dụng định lý sin trong tam giác, ta có
U sin β = U d sin α → 271 sin 150 0 = 125 sin α → α ≈ 9 0 .
→ Vậy độ lệch pha giữa điện áp hai đầu mạch là φ = 30 0 + α = 39 0
Đáp án C

Bài 1:
Để công suát tiêu thụ trê mạch cực đại thì:
\((R+r)^2=(R_1+r)(R_1+r)\)
\(\Rightarrow (R+10)^2=(15+10)(39+10)\)
\(\Rightarrow R=25\Omega\)
Bài 2: Có hình vẽ không bạn? Vôn kế đo hiệu điện thế của gì vậy?


Chọn đáp án C