Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2) Ta có:
\(B=x^4+2x^3y-2x^3+x^2y^2-2x^2y-x\left(x+y\right)+2x+3\)
\(=x^4+x^3y-2x^3+x^3y+x^2y^2-2x^2y-x\left(x+y\right)+2x+3\)
\(=\left(x^4+x^3y-2x^3\right)+\left(x^3y+x^2y^2-2x^2y\right)-\left[x\left(x+y\right)-2x\right]+3\)
Do \(x+y-2=0\Rightarrow x+y=2\)
\(\Rightarrow B=\left(x^4+x^3y-2x^3\right)+\left(x^3y+x^2y^2-2x^2y\right)-\left[2x-2x\right]+3\)
\(=x^3.\left(x+y-2\right)+x^2y\left(x+y-2\right)-0+3\)
\(=0+0+3\)
\(=3\)
Vậy \(B=3\)
1) Ta có:
\(A=x^3+x^2y-2x^2-xy-y^2+3y+x-1\)
\(=\left(x^3+x^2y-2x^2\right)-\left(xy+y^2-2y\right)+y+x-1\)
\(=x^2\left(x+y-2\right)-y\left(x+y-2\right)+\left(x+y-2\right)+1\)
\(=0+0+0+1\)
\(=1\)
Vậy \(A=1\)

a, Ta có: \(\left|x-\dfrac{2}{7}\right|\ge0\forall x\)
\(\Rightarrow\left|x-\dfrac{2}{7}\right|+0,5\ge0,5\forall x\)
Hay: \(A\ge0,5\forall x\)
=> Min A = 0,5 tại \(\left|x-\dfrac{2}{7}\right|=0\Rightarrow x=\dfrac{2}{7}\)
b, \(B=\left|x-5\right|+\left|x-2\right|=\left|x-5\right|+\left|2-x\right|\ge\left|x-5+2-x\right|\) =3
=> Min B = 3 tại \(\left(x-5\right)\left(2-x\right)>0\)
=)) Làm nốt
c,Tương tự b
=.= hk tốt!!

a)A=x+3/x-2
A=x-2+5/x-2
A=1+5/x-2
vì 1 thuộc Z nên để A thuộc Z thì 5 phải chia hết cho x-2
x-2 thuộc ước của 5
x-2 thuộc -5;-1;1;5
x = -3;1;3 hoặc 7
giá trị các biểu thức theo giá trị của x như trên và lần lượt là 0;-4;6;2
b)để B= 1-2x/2+x thuộc Z thì
1-2x phải chia hết cho 2+x
nên 1-2x-4+4 phải chia hết cho x+2
1-(2x+4)+4 phải chia hết cho x+2
1+4-[2(x+2] phải chia hết cho x+2
5 -[2(x+2] phải chia hết cho x+2
vì [2(x+2] chia hết cho x+2 nên 5 phải chia hết cho x+2
suy ra x+2 thuộc ước của 5
x+2 thuộc -5;-1;1;5
x=-7;-3;-1;3
giá trị các biểu thức theo giá trị của x như trên và lần lượt là -3;-7;3;-1

a) Phương trình hoành độ giao điểm f(x) = X2 - x - 2 =0 ⇔ x = -1 hoặc x = 2.
Diện tích hình phẳng cần tìm là :
b) Phương trình hoành độ giao điểm:
f(x) = 1 - ln|x| = 0 ⇔ lnx = ± 1
⇔ x = e hoặc
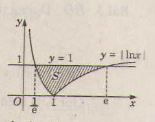
y = ln|x| = lnx nếu lnx ≥ 0 tức là x ≥ 1.
hoặc y = ln|x| = - lnx nếu x < 0, tức là 0 < x < 1.
Dựa vào đồ thị hàm số vẽ ở hình trên ta có diện tích cần tìm là :
Ta có ∫lnxdx = xlnx - ∫dx = xlnx – x + C, thay vào trên ta được :
c) Phương trình hoành độ giao điểm là:
f(x) = 6x – x2 – (x - 6)2 = -2(x2 – 9x +18)
f(x) = 0 ⇔ -2(x2 – 9x +18) ⇔ x = 3 hoặc x = 6.
Diện tích cần tìm là:

Câu 1:
\(AB=\sqrt{\left[3-\left(-2\right)\right]^2+\left(3-2\right)^2}=\sqrt{26}\)
\(BC=\sqrt{\left(2-3\right)^2+\left(-2-3\right)^2}=\sqrt{26}\)
\(AC=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-2-2\right)^2}=4\sqrt{2}\)
\(P=\dfrac{AB+BC+AC}{2}=\dfrac{2\sqrt{26}+4\sqrt{2}}{2}=\sqrt{26}+2\sqrt{2}\)
\(S=\sqrt{\left(\sqrt{26}+2\sqrt{2}\right)\cdot2\sqrt{2}\cdot2\sqrt{2}\cdot\left(\sqrt{26}-2\sqrt{2}\right)}=\sqrt{18\cdot8}=12\left(đvdt\right)\)

a) Ta có:
\(M\left(x\right)=A\left(x\right)-2.B\left(x\right)+C\left(x\right)\)
\(=\left(2x^5-4x^3+x^2-2x+2\right)-2.\left(x^5-2x^4+x^2-5x+3\right)+\left(x^4+3x^3+3x^2-8x+4\frac{3}{16}\right)\)
\(=2x^5-4x^3+x^2-2x+2-2x^5+4x^4-2x^2+10x-6+x^4+4x^3+3x^2-8x+\frac{67}{16}\)
\(=\left(2x^5-2x^5\right)+\left(4x^4+x^4\right)+\left(-4x^3+4x^3\right)+\left(x^2-2x^2+3x^2\right)+\left(-2x+10x-8x\right)+\left(2-6+\frac{67}{16}\right)\)
\(=0+5x^4+0+2x^2+0+\frac{3}{16}\)
\(=5x^4+2x^2+\frac{3}{16}\)
b) Thay \(x=-\sqrt{0,25}=-0,5\); ta có:
\(M\left(-0,5\right)=5.\left(-0,5\right)^4+2.\left(-0,5\right)^2+\frac{3}{16}\)
\(=5.0,0625+2.0,25+\frac{3}{16}\)
\(=\frac{5}{16}+\frac{8}{16}+\frac{3}{16}=\frac{16}{16}=1\)
c) Ta có:
\(x^4\ge0\) với mọi x
\(x^2\ge0\) với mọi x
\(\Rightarrow5x^4+2x^2+\frac{3}{16}>0\) với mọi x
Do đó không có x để M(x)=0
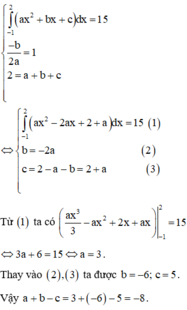

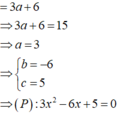
Đáp án C
Ta có S = ∫ 1 e 1 + ln x x d x . Đặt 1 + ln x = t ⇒ ln x = t 2 − 1 ⇒ 1 x = d x = 2 t d t
Đổi cận: x = 1 ⇒ t = 1 ; x = e ⇒ t = 2
⇒ S = ∫ 1 2 t .2 t d t = 2 t 3 3 2 1 = 4 2 3 − 2 3 = 4 2 − 2 3 ⇒ a = 4 3 b = − 2 3
⇒ a 2 + b 2 = 16 9 + 4 9 = 20 9