Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự kẻ hình nha .
a) Chiều cao hình thang ABCD là :
50 x 2 : 16 = 6,25 ( cm )
Diện tích hình thang ABCD là :
( 9 + 16 ) x 6,25 : 2 = 78,125 (cm2)
b) Diện tích BMC = diện tích AMD vì diện tích tam giác ABC = diện tích tam giác BDA . Vì hai tam giác bằng nhau cùng trừ đi tam giác MBA .
Ta có tam giác BMC = tam giác BAC nên tỉ số \(\frac{MB}{MD}\)\(=\)\(\frac{AM}{MC}\)

A B C D M N
Ta có: \(S_{AMN}=\frac{BN.AM}{2}=\frac{BN\cdot\frac{1}{2}AB}{2}\)
\(S_{ABN}=\frac{AB.BN}{2}\)
=> \(\frac{S_{AMN}}{S_{ABN}}=\frac{\frac{\frac{1}{2}BN.AB}{2}}{\frac{AB.BN}{2}}=\frac{1}{2}\) => \(S_{AMN}=\frac{1}{2}S_{ABN}\)(1)
Ta lại có: BN = 2NC; BN + NC = BC => BN = 2/3BC
\(S_{ABN}=\frac{AB.BN}{2}=\frac{AB\cdot\frac{2}{3}BC}{2}\)
\(S_{ABCD}=AB.BC\)
\(\frac{S_{ABN}}{S_{ABCD}}=\frac{\frac{\frac{2}{3}AB.BC}{2}}{AB.BC}=\frac{1}{3}\) => \(S_{ABN}=\frac{1}{3}S_{ABCD}\) => \(\frac{1}{2}S_{ABN}=\frac{1}{6}S_{ABCD}\)(2)
Từ (1) và (2) => \(S_{AMN}=\frac{1}{6}S_{ABCD}\)
awbb ưieaaaaaaaa
r
ewfrsd
tf
sdfdyufee
e
ẻ
r
re
ê
r
e
ẻ
e
re
ẻ
rr
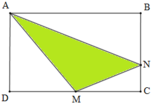
Theo đề bài:
M C = M D ⇒ M C = M D = 1 2 D C B N = 2 3 B C ⇒ N C = 1 3 B C
Ta có:
S A D M = 1 2 × A D × D M = 1 2 × A D × D C 2 = 1 4 × A D × D C
Suy ra diện tích tam giác ADM bằng 1 4 diện tích hình chữ nhật ABCD.
Diện tích tam giác ADM là: 96 : 4 = 24 ( c m 2 )
S A B N = 1 2 × A B × B N = 1 2 × A B × 2 3 B C = 1 3 × A B × B C
Suy ra diện tích tam giác ABN bằng 1 3 diện tích hình chữ nhật ABCD.
Diện tích tam giác ABN là: 96 : 3 = 32 ( c m 2 )
S M N C = 1 2 × M C × N C = 1 2 × 1 2 D C × 1 3 B C = 1 12 × D C × B C
Suy ra diện tích tam giác MNC bằng 1 12 diện tích hình chữ nhật ABCD.
Diện tích tam giác MNC là: 96 : 12 = 8 ( c m 2 )
Diện tích tam giác AMN là: 96 − ( 24 + 32 + 8 ) = 32 ( c m 2 )
Đáp số: 32 c m 2
Vậy đáp án đúng điền vào ô trống là 32.