Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(23,3\) phút; \(540^0;27,6^0C\)
b) Khi lấy số trung bình làm đại diện cho các số liệu thống kê về quy mô và độ lớn, có thể xem rằng mỗi ngày bạn A đi từ nhà đến trường đều mất 23,3 phút.
Tương tự, nêu ý nghĩa số trung bình của các số liệu thống kê cho ở bảng 7 và bảng 8.

a) Tính chiều cao trung bình của học sinh nam
Cách 1 : Sử dụng bảng phân bố tần số ghép lớp :
\(\overline{x}=\dfrac{1}{60}\left(5.140+9.150+19.160+17.170+10.180\right)\)
\(\overline{x}=163\)
Cách 2 : Sử dụng bảng phân bố tần suất ghép lớp :
\(\overline{x}=\dfrac{1}{100}\left(8,33.140+15.150+31,67.160+28,33.170+16,67.180\right)\)\(\overline{x}=163\)
Tính chiều cao trung bình của học sinh nữ:
Cách 1 : Sử dụng bảng phân bố tần số ghép lớp \(\overline{x}=\dfrac{1}{60}\left(8.140+15.150+16.160+14.170+7.180\right)\)
\(\overline{x}=159,5\)
Cách 2 : Sử dụng bảng phân bố tần suất ghép lớp :
\(\overline{x}=\dfrac{1}{100}\left(13,33.140+25.150+26,67.160+23,33.170+11,67.180\right)\)
\(\overline{x}=159,5\)
b) Vì \(\overline{x}_{nam}=163>\overline{x}_{nữ}=159,5\) nên suy ra học sinh ở nhóm nam cao hơn học sinh ở nhóm nữ
c) \(\overline{x}=\left(60.159,5+60.163\right)\dfrac{1}{2}\approx161\left(cm\right)\)

a)Số học sinh giỏi lớp 6a là:
40x22,5%=9(học sinh)
Số học sinh trung bình lớp 6a là:
9x200%=18(học sịnh)
Số học sinh khá lớp 6a là:
40-(9+18)=13(học sinh)
b)Tỉ số phần trăm số học sinh trung binh so với cả lớp là:
18:40%=45(%)
Tỉ số phần trăm số học sinh khá so với cả lớp là:
13:40%=32,5(%)

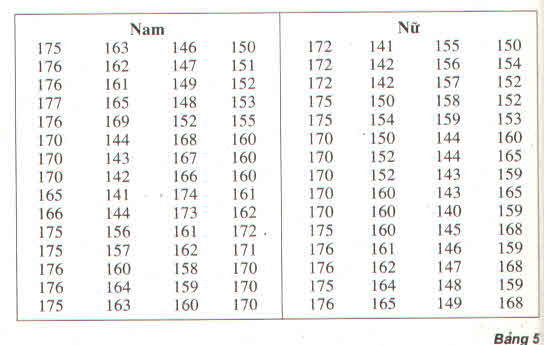
a) Dãy các số liệu chiều cao của các học sinh nam ở bảng 5 có :
\(\overline{x_1}\approx163\left(cm\right);s_1^2\approx134,3;s_1\approx11,59\)
Dãy các số liệu chiều cao của các học sinh nữ cho ở bảng 5 có :
\(\overline{x_2}\approx159,5\left(cm\right);s_2^2\approx148;s_2\approx12,17\)
b) Nhóm T có \(\overline{x_3}=163\left(cm\right);s_3^2=169;s_3=13\)
Học sinh ở nhóm nam và nhóm T có chiều cao như nhau và cùng lớn hơn chiều cao của học sinh ở nhóm nữ (vì \(\overline{x}_1=\overline{x}_3>\overline{x}_2\)
Vì \(\overline{x}_1=\overline{x}_3=163\left(cm\right)\) và \(s_1< s_3\) nên chiều cao của các học sinh nam đồng đều hơn chiều cao của các học sinh nhóm T

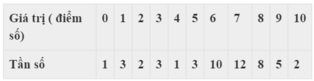
a) Điểm số của xạ thủ A có : \(\overline{x}\approx8,3\) điểm ; \(s_1^2\approx1,6;s_1\approx1,27\) điểm
Điểm số của xạ thủ B có \(\overline{y}=8,4\) điểm, \(s_2^2\approx1,77;s_2\approx1,33\) điểm
b) \(\overline{x}\approx\overline{y}=8,4\) điểm; \(s_1^2< s_2^2\), như vậy mức độ phân tán của các điểm số (so với số trung bình) của xạ thủ A là bé hơn. Vì vậy trong lần tập bắn này xạ thủ A bắn chụm hơn.

C1:
\(A=\dfrac{10^{50}+2}{10^{50}-1}=\dfrac{10^{50}-1}{10^{50}-1}+\dfrac{3}{10^{50}-1}=1+\dfrac{3}{10^{50}-1}\\ B=\dfrac{10^{50}}{10^{50}-3}=\dfrac{10^{50}-3}{10^{50}-3}+\dfrac{3}{10^{50}-3}=1+\dfrac{3}{10^{50}-3}\\ \text{Vì }10^{50}-3< 10^{50}-1\Rightarrow\dfrac{3}{10^{50}-3}>\dfrac{3}{10^{50}-1}\Rightarrow1+\dfrac{3}{10^{50}-3}>1+\dfrac{3}{10^{50}-1}\Leftrightarrow B>A\)
Vậy \(B>A\)
C2: Áp dụng \(\dfrac{a}{b}>1\Rightarrow\dfrac{a}{b}>\dfrac{a+n}{b+n}\left(n>0\right)\)
Dễ thấy
\(B=\dfrac{10^{50}}{10^{50}-3}>1\\ \Rightarrow B=\dfrac{10^{50}}{10^{50}-3}>\dfrac{10^{50}+2}{10^{50}-3+2}=\dfrac{10^{50}+2}{10^{50}-1}=A\)
Vậy \(B>A\)


c) Trong 60 buổi được khảo sát
Chiếm tỉ lệ thấp nhất (8,33%) là những buổi có dưới 10 người xem
Chiếm tỉ lệ cao nhất (25%) là những buổi có từ 30 người đến dưới 40 người xem
Đa số (78,33%) các buổi có từ 10 người đến dưới 50 người xem
d) \(\overline{x}\approx32\) người; \(s^2\approx219,7;s=15\) người








Đáp án: D
Ta có: