Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ta có :
\(\Delta'=1^2-\left(-1-m\right)\left(m^2-1\right)=1-\left(-m^2+1-m^3+m\right)=1+m^2-1+m^3-m=m^3+m^2-m=m\left(m^2+m-1\right)\)để phương trình có nghiệm thì \(\Delta\ge0\)
hay \(m\left(m^2+m-1\right)\ge0\)
=> \(\left\{{}\begin{matrix}m\ge0\\m^2+m-1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2-\dfrac{5}{4}\ge0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2\ge\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left[{}\begin{matrix}m+\dfrac{1}{2}\ge\\m+\dfrac{1}{2}\le-\dfrac{\sqrt{5}}{2}\end{matrix}\right.\end{matrix}\right.\dfrac{\sqrt{5}}{2}}\)

Ta có : \(0< \alpha< \dfrac{\pi}{2}\)
=> \(\sin\alpha>0,\cos\alpha>\text{0},\tan\alpha>\text{0},\cot\alpha>\text{0}\)
a, Ta có : \(\sin\left(\alpha-\pi\right)=-\sin\left(\pi-\alpha\right)=-\left[-\sin\left(\alpha\right)\right]=\sin\alpha\)
=> \(sin\left(\alpha-\pi\right)>\text{0}\)
b, \(\cos\left(\dfrac{3\pi}{2}-\alpha\right)=\cos\left(\pi+\dfrac{\pi}{2}-\alpha\right)=-\cos\left(\dfrac{\pi}{2}-\alpha\right)=-sin\alpha\)
=> \(\cos\left(\dfrac{3\pi}{2}-\alpha\right)< \text{0}\)
c, \(tan\left(\alpha+\pi\right)=tan\alpha\)
=> \(tan\left(\alpha+\pi\right)>\text{0}\)
d, \(cot\left(\alpha+\dfrac{\pi}{2}\right)=-tan\alpha\)
=> \(cot\left(\alpha+\dfrac{\pi}{2}\right)< \text{0}\)

Bài 1a)
Áp dụng bất đẳng thức Cô-si cho từng cặp ta có
\(\left\{\begin{matrix}a+b\ge2\sqrt{ab}\\b+c\ge2\sqrt{bc}\\c+a\ge2\sqrt{ac}\end{matrix}\right.\)
\(=>\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge2\sqrt{ab}.2\sqrt{bc}.2\sqrt{ac}\)
\(=>\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\sqrt{\left(abc\right)^2}\)
\(=>\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8abc\) ( điều phải chứng minh )
Bài 1b)
Áp dụng bất đẳng thức Cô-si bộ 3 số cho từng cặp ta có
\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\a^2+b^2+c^2\ge3\sqrt[3]{\left(abc\right)^2}\end{matrix}\right.\)
\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\left(abc\right)^2}\)
\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge9\sqrt[3]{\left(abc\right)^3}\)
\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge9abc\) (điều phải chứng minh )
Bài 1c) Ta có
\(\left(1+a\right)\left(1+b\right)\left(1+c\right)\ge\left(1+\sqrt[3]{abc}\right)^3\)
\(=>1+a+b\left(1+a\right)\left(1+c\right)\ge1^3+3.1^2.\sqrt[3]{abc}+3.1.\sqrt[3]{\left(abc\right)^2}+\sqrt[3]{\left(abc\right)^3}\)
\(=>\left(1+a+b+ab\right)\left(1+c\right)\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)
\(=>1+a+b+ab+c\left(1+a+b+ab\right)\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)
\(=>1+a+b+ab+c+ca+bc+abc\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)
\(=>a+b+c+ab+bc+ca\ge3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}\)
Áp dụng bất đẳng thức Cô-si bộ 3 số cho vế trái ta có
\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\ab+bc+ac\ge3\sqrt[3]{\left(abc\right)^2}\end{matrix}\right.\)
\(=>a+b+c+ab+bc+ac\ge3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}\) (điều phải chứng minh )
Bài 2a)
Áp dụng bất đẳng thức Cô-si cho từng cặp ta có
\(\left\{\begin{matrix}\frac{bc}{a}+\frac{ca}{b}\ge2\sqrt{\frac{bc}{a}.\frac{ca}{b}}=2\sqrt{c^2}=2c\\\frac{ca}{b}+\frac{ab}{c}\ge2\sqrt{\frac{ca}{b}.\frac{ab}{c}}=2\sqrt{a^2}=2a\\\frac{bc}{a}+\frac{ab}{c}\ge2\sqrt{\frac{bc}{a}.\frac{ab}{c}}=2\sqrt{b^2}=2b\end{matrix}\right.\)
\(=>2\left(\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\right)\ge2\left(a+b+c\right)\)
\(=>\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\ge a+b+c\) (điều phải chứng minh )
Bài 2b)
Chứng minh BĐT \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
Áp dụng BĐT Cô-si cho vế trái ta có
\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\sqrt[3]{\frac{1}{abc}}\end{matrix}\right.\)
\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\frac{1}{abc}}\)
\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9.\sqrt[3]{\frac{abc}{abc}}\)
\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\) (điều phải chứng minh )
Ta có \(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\ge\frac{3}{2}\)
\(=>\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}+3\ge\frac{3}{2}+3\)
\(=>\frac{a}{b+c}+1+\frac{b}{a+c}+1+\frac{c}{a+b}+1\ge\frac{9}{2}\)
\(=>\frac{a+b+c}{b+c}+\frac{a+b+c}{a+c}+\frac{a+b+c}{a+b}\ge\frac{9}{2}\)
\(=>\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge\frac{9}{2}\)
\(=>2\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge9\)
Áp dụng BĐT vừa chứng minh \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
\(=>\left(b+c+a+c+a+b\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge9 \) (Điều phải chứng minh )

\(x^2-5x+6\le0\Rightarrow2\le x\le3\)
\(\left|x-m\right|>1\Rightarrow\left[{}\begin{matrix}x-m>1\\x-m< -1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m< x-1\\m>x+1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m< 2\\m>3\end{matrix}\right.\)
\(\Rightarrow\) Để hệ vô nghiệm thì \(2\le m\le3\)

3.
\(\left|2x-4\right|< 10\Leftrightarrow-10< 2x-4< 10\)
\(\Leftrightarrow-3< x< 7\)
\(\Rightarrow C=\left(-3;7\right)\)
\(\left|-3x+5\right|>8\Rightarrow\left[{}\begin{matrix}-3x+5>8\\-3x+5< -8\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x< -1\\x>\frac{13}{3}\end{matrix}\right.\) \(\Rightarrow D=\left(-\infty;-1\right)\cup\left(\frac{13}{3};+\infty\right)\)
\(\Rightarrow C\cap D=\left(-3;-1\right)\cap\left(\frac{13}{3};7\right)\)
\(\Rightarrow\left(C\cap\right)D\cup E=\left(-3;7\right)\)
4.
Hình như cái đề chẳng liên quan gì đến đáp án hết :)
1.
\(A\cap B\ne\varnothing\Leftrightarrow\left\{{}\begin{matrix}2m-1\le m+2\\2m+3\ge m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\le3\\m\ge-3\end{matrix}\right.\) \(\Rightarrow-3\le m\le3\)
2.
\(\frac{5}{\left|2x-1\right|}>2\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{1}{2}\\\left|2x-1\right|< \frac{5}{2}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{1}{2}\\-\frac{5}{2}< 2x-1< \frac{5}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{1}{2}\\-\frac{3}{4}< x< \frac{7}{4}\end{matrix}\right.\)
Rất tiếc tập này không thể liệt kê được (có vô số phần tử)

a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)

\(\Delta_1\) nhận \(\left(2;1\right)\) là 1 vppt; \(\Delta_2\) nhận \(\left(1;m\right)\) là 1 vtpt
a/ Để 2 đường thẳng song song \(\Rightarrow2m=1\Rightarrow m=\frac{1}{2}\)
Khi đó pt \(\Delta_2\) viết lại: \(2x+y+2=0\)
Khoảng cách 2 đường thẳng: \(d=\frac{\left|c_1-c_2\right|}{\sqrt{a^2+b^2}}=\frac{\left|-3-2\right|}{\sqrt{2^2+1^2}}=\sqrt{5}\)
b/Với \(m=2\Rightarrow\Delta_2\) nhận \(\left(1;2\right)\) là 1 vtpt
\(cos\left(\Delta_1;\Delta_2\right)=\frac{\left|2.1+1.2\right|}{\sqrt{2^2+1^2}.\sqrt{1^2+2^2}}=\frac{4}{5}\)
\(\Rightarrow sin\left(\Delta_1;\Delta_2\right)=\sqrt{1-\left(\frac{4}{5}\right)^2}=\frac{3}{5}\)
c/ Chắc là k/c từ gốc O
\(d\left(O;\Delta_1\right)=\frac{\left|2.0+1.0-3\right|}{\sqrt{2^2+1^2}}=\frac{3}{\sqrt{5}}\)
\(d\left(O;\Delta_2\right)=\frac{\left|1.0+m.0+1\right|}{\sqrt{1+m^2}}=\frac{1}{\sqrt{1+m^2}}\)
\(\Rightarrow\frac{1}{\sqrt{1+m^2}}=\frac{6}{\sqrt{5}}\Leftrightarrow1+m^2=\frac{5}{36}\Leftrightarrow m^2=-\frac{29}{36}< 0\)
Không tồn tại m thỏa mãn
d/ I là điểm nào bạn?

\(a=-1< 0;\) \(-\frac{b}{2a}=1\in\left[-1;2\right]\)
\(\Rightarrow\) Hàm số đạt GTLN tại \(\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
\(y\left(-1\right)=m-7\) ; \(y\left(2\right)=m-12\)
Do \(m-7>m-12\) \(\forall m\)
\(\Rightarrow\max\limits_{\left[-1;2\right]}y=y\left(-1\right)\Rightarrow m-7=3\Rightarrow m=10\)
Đáp án D



Chọn C.
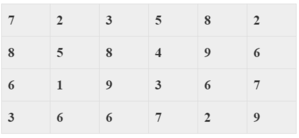
Lập bảng tần số:
Ta thấy điểm 6 có tần số lớn nhất nên Mo = 6