Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trên tia đối của tia MA , lấy D sao cho MA=MD
Xét 2 tg MAB và tg MDC , ta có : MA=MD ; MB=MC(vì M là trung điểm của BC) ; MAB=CMD(vì đối đỉnh)
->tg MAB =tg MDC (c.g.c) -> AB=CD (2 cạnh tương ứng) và MAB = CDM (2 góc tương ứng)
Ta có AB<AC(gt) -> CD<AC
Trong tg ACD , vì AC<CD ->CDM<CAM ( quan hệ giữa cạnh với góc đối diện) -> BAM<CAM

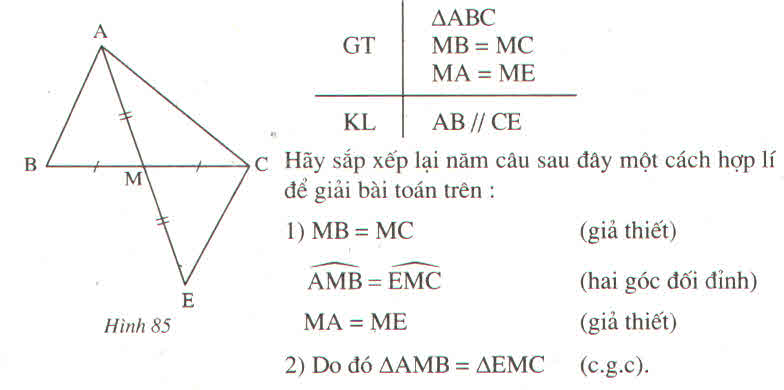
a) Xét tam giác ABM và tam giác ECM có :
AM = ME
\(\widehat{AMB}=\widehat{CME}\left(đđ\right)\)
BM = MC
\(\Rightarrow\) tam giác ABM = tam giác ECM ( c-g-c ) (đpcm)
b) Do tam giác ABM = tam giác ECM
\(\Rightarrow AB=CE\) (1)
Mà tam giác ABC vuông tại B
\(\Rightarrow AC>AB\) ( do cạnh AC là cạnh huyền ) (2)
Từ (1) và (2) \(\Rightarrow AC>CE\left(đpcm\right)\)
c) Xét tam giác ACE có : \(AC>CE\)
\(\Rightarrow\widehat{MAC}< \widehat{CEA}\left(3\right)\)
Mà tam giác ABM = tam giác ECM ( câu a )
\(\Rightarrow\widehat{BAM}=\widehat{CEA}\left(4\right)\)
Từ (3) và (4) \(\Rightarrow\widehat{BAM}>\widehat{MAC}\left(đpcm\right)\)

a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: BA//DC
=>\(\widehat{BAM}=\widehat{CDM}\)
b: Ta có: \(\widehat{BAM}=\widehat{CDM}\)
mà \(\widehat{CDM}>\widehat{MAC}\)(DA>DC)
nên \(\widehat{BAM}>\widehat{MAC}\)
Trên tia đối của tia MA lấy N sao cho NM = MA
Xét \(\Delta\)MAB và \(\Delta\)MNC có :
\(\Rightarrow\)\(\Delta\)MAB = \(\Delta\)MNC ( c - g - c )
\(\Rightarrow\)CN = AB ( hai cạnh tương ứng )
Mà AB < AC \(\Rightarrow\)CN < AC
\(\Rightarrow\)MÂC < góc ANC
Mà góc ANC = BÂM ( vì\(\Delta\)MAB = \(\Delta\)MNC )
\(\Rightarrow\)MÂB > MÂC ( đpcm )