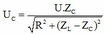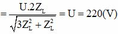Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giải thích: Đáp án C
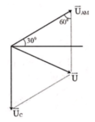
+ Vẽ giản đồ vectơ như hình vẽ
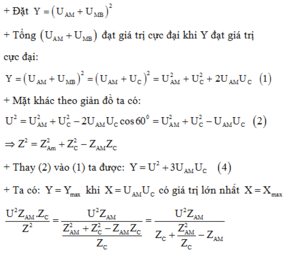
X = Xmax khi mẫu số cực tiểu, suy ra:
+ Từ (4) và (5):
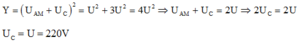
Giải thích: Đáp án B
Độ lệch pha giữa hai đầu đoạn mạch AM:
Tổng trở của mạch AM:
Đặt 
Tổng (UAM + UMB) đạt giá trị cực đại khi Y đạt giá trị cực đại
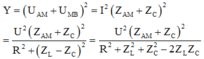
Để Y = Ymax thì đạo hàm của Y theo ZC phải bằng không:
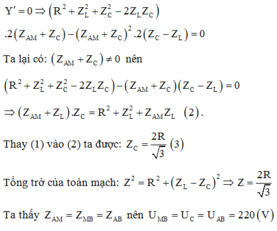
+ \(U_{AM}=I.Z_{AM}\), \(Z_{AM}\)không thay đổi, nên để \(U_{AM}\) đạt giá trị lớn nhất khi thay đổi C thì dòng điện Imax --> Xảy ra hiện tượng cộng hưởng: \(Z_L=Z_C\)
và \(I=\frac{U}{R+r}\)
Công suất của cuộn dây khi đó: \(P=I^2.r=\left(\frac{U}{R+r}\right)^2.r\) (*)
+ Nếu đặt vào 2 đầu AB một điện áp không đổi và nối tắt tụ C thì mạch chỉ gồm r nối tiếp với R (L không có tác dụng gì)
Cường độ dòng điện của mạch: \(I=\frac{25}{R+r}=0,5\Rightarrow R+r=50\)
Mà R = 40 suy ra r = 10.
Thay vào (*) ta đc \(P=\left(\frac{200}{50}\right)^2.10=160W\)
Bạn học đến điện xoay chiều rồi à. Học nhanh vậy, mình vẫn đang ở dao động cơ :(
\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V
Đáp án C
Biểu diễn vecto các điện áp: U A M → hợp với phương ngang của dòng điện một góc 30 0 , U M B → chứa tụ nên hướng thẳng đứng xuống dưới, U → = U A M → + U M B →
+ Áp dụng định lý sin trong tam giác, ta có:
=> 
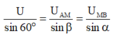
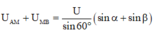
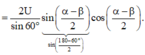
=> Ta thấy rằng tổng UAM + UMB cực đại khi α = β = 0 , 8 ( 180 0 - 60 0 ) = 60 0
=> Các vecto hợp thành tam giác đều => U C = 220 V
Đáp án C.
lúc đầu ta có :
UMB=2UR => ZMB=2R <=> ZC=\(\sqrt{3}\)R mà C=\(\frac{L}{R^2}\) => ZL=\(\frac{R}{\sqrt{3}}\)
lúc sau ta có Uc' max :
Zc'.ZL=R2+ \(Z^2_L\) => Zc'=\(\frac{4R}{\sqrt{3}}\)
\(\text{tanφ}=\frac{Z_L-Z_C}{R}\Rightarrow\tan\varphi=-\sqrt{3}\Rightarrow\varphi=-\frac{\pi}{3}\)
Đáp án A
Vì φ A M = π/6 nên suy ra đoạn AM có R và L, đồng thời có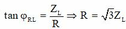
Ta có
Xé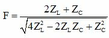t
Đặt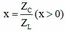 
ta có: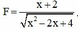 
Khảo sát hàm số với x > 0, ta tìm được Max F = 2 khi và chỉ khi x = 2. Suy ra U A M + U M B lớn nhất khi Z C = 2 Z L
Khi đó
