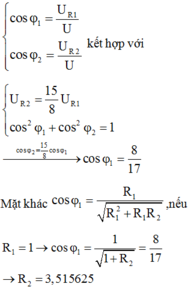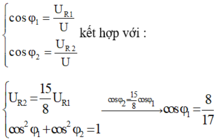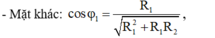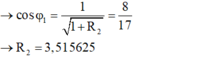Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng kết quả chuẩn hóa của bài toán ω thay đổi để điện áp hiệu dụng trên tụ điện cực đại, khi đó Z L = 1 Z C = n R = 2 n − 2
→ U L = 0 , 1 U R ⇔ Z L = 0 , 1 R ⇔ 1 = 0 , 1 2 n − 2
→ n = 51
Hệ số công suất của mạch khi đó
cos φ = 2 1 + n = 2 1 + 51 = 1 26
Đáp án D

Bạn áp dụng kết quả này của mạch RLC khi $w$ thay đổi để $U_C$max nhé:
\(\tan\varphi_{RL}.\tan\varphi_{mạch}=0,5\)
\(\tan\varphi_{RL}=\frac{Z_L}{R}=\frac{U_L}{U_R}=0,1\)
\(\Rightarrow\tan\varphi_{mạch}=5\)
\(\Rightarrow\cos\varphi=\frac{1}{\sqrt{1+\tan^2\varphi}}=\frac{1}{\sqrt{26}}\)

Chọn C
UC = UCmax khi ω = 1 L L C - R 2 2 (1) và UCmax= 2 U L R 4 L C - R 2 C 2 (*)
Khi đó ZL = ωL = L C - R 2 2 ; ZC = 1 C ω = L C 1 L C - R 2 2
URL = U R 2 + Z L 2 R 2 + ( Z L - Z C ) 2 ; UCmax= U Z C R 2 + ( Z L - Z C ) 2
=> U R L U C m a x = R 2 + Z L 2 Z C = 5 3
=> 9 R 2 + Z L 2 =5 Z C 2 => 9(R2 + L C - R 2 2 ) = 5 Z C 2
=> 9( L C + R 2 2 )C2( L C - R 2 2 ) =5L2 => 9C2( L 2 C 2 - R 4 4 ) = 5L2
=> 4L2 = 9 R 4 C 2 4 => 4L= 3R2C (**)
UCmax = 2 U L R 4 L C - R 2 C 2 = 2 U L R C ( 4 L - R 2 C ) = 2 U L R 2 C R 2 C = 2 U 2 L R 2 C
= 2 U 2 . 3 4 = 90V
=> U = 60 2 (V)

Bạn áp dụng kết quả này của bài toán mạch RLC có C thay đổi để Uc max:
umạch vuông pha với uRL
Ta có giản đồ véc tơ sau:
U U U RL C m i 120 120√3 φ φ
Từ giản đồ véc tơ: \(U_{RL}=\sqrt{3.120^2-120^2}=120\sqrt 2(V)\)
Suy ra hệ số công suất: \(\cos\varphi=\dfrac{U_{RL}}{U_C}=\dfrac{120\sqrt 2}{120\sqrt 3}=\sqrt{\dfrac{2}{3}}\)