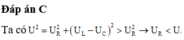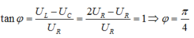Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Đáp án C.
lúc đầu ta có :
UMB=2UR => ZMB=2R <=> ZC=\(\sqrt{3}\)R mà C=\(\frac{L}{R^2}\) => ZL=\(\frac{R}{\sqrt{3}}\)
lúc sau ta có Uc' max :
Zc'.ZL=R2+ \(Z^2_L\) => Zc'=\(\frac{4R}{\sqrt{3}}\)
\(\text{tanφ}=\frac{Z_L-Z_C}{R}\Rightarrow\tan\varphi=-\sqrt{3}\Rightarrow\varphi=-\frac{\pi}{3}\)

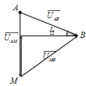
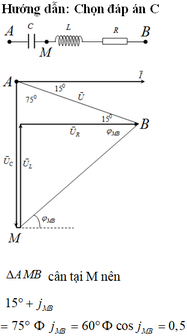
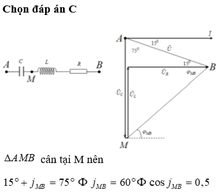
Biểu diễn vecto các điện áp. Vì U A M = U M B → AMB là tam giác cân tại M.
Từ giản đồ, ta có A ^ = B ^ = 90 0 − 15 0 = 75 0
→ φ M B = 75 0 − 15 0 = 60 0 → cos φ M B = 1 2
Đáp án C

Xét đoạn mạch MB có điện áp hiệu dụng gấp đôi điện áp hiệu dung trên R suy ra góc giữa \(U_{MB}\) và \(i\) là \(60^0\)
Mà \(u\) lệch pha \(90^0\) so với \(u_{MB}\)
Suy ra độ lệch pha giữa u và i là \(\varphi =30^0\)
Ta có:
\(P=U. I. \cos \varphi=120\sqrt 3.0,5.\cos30^0=90W\)

Đáp án A
L = L1, i cùng pha u => cộng hưởng ⇒ Z L 1 = Z C
L = L2, UL max ⇒ Z L 2 = R 2 + Z C 2 Z C
Để ý thấy L2 = 2L1. Thay R = 50 vào, ta có hệ: Z L 2 = 50 2 + Z C 2 Z C Z L 1 = Z C Z L 2 = 2 Z L 1 ⇔ Z L 1 = 50 Z L 2 = 100 Z C = 50 3
Từ đó dễ dàng tìm được f = 25(Hz).