Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Cơ năng của con lắc là: W = 1 2 k x 2 + 1 2 m v 2 = 1 2 k 0 , 045 − Δ l 2 + 1 2 m v 2
+ Mà Δ l = m g k
® 2 W = k 0 , 045 − m g k 2 + m .0 , 4 2 = 80.10 − 3
+ Giải phương trình trên ta được: m = 0 , 25 g m = 0 , 49 g ® chọn m = 0 , 25 g
+ T = 2 π m k = 2 π 0 , 25 100 = π 10 s
Đáp án B

+ Cơ năng của con lắc là:

+ Mà ∆ l = m g k
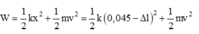
+ Giải phương trình trên ta được: m = 0 , 25 m = 0 , 49 → chọn m = 0,25 g
T = 2 π m k = 2 π 0 . 25 100 = π 10 s
ü Đáp án B

\(W = \frac{1}{2} kA^2 => A^2 = \frac{2W}{k} = 8.10^{-4}m^2.\)
Độ dãn của lo xo tại vị trí cân bằng \(\Delta l = \frac{mg}{k}\)
Từ VTCB kéo tới vị trí lò xo dãn 4,5 cm tức là li độ x của lò xo (so với VTCB) là: \(x = 4,5.10^{-2} - \Delta l\)
\(A^2 = x^2 +\frac{v^2}{\omega^2}\)
=> \(8.10^{-4} = (4,5.10^{-2} - \frac{m.10}{100})^2 + \frac{m.0,4^2}{100}\)
=> \(0,01 m^2 - 7,4.10^{-3} m + 1,225.10^{-3} = 0\)
=> \(m = 0,49 kg; \) (loại) hoặc \(m = 0,25 kg; \)(chọn)
=> \(T = 2\pi \sqrt{\frac{m}{k}} = 2\pi \sqrt{\frac{0,25}{100}} = 0,1\pi.(s)\)

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)
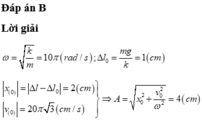

ü Đáp án B
+ Cơ năng của con lắc là:
+ Giải phương trình trên ta được: m = 0 , 25 m = 0 , 49 → c h ọ n m = 0 , 25
T = 2 π m k = 2 π 0 . 25 100 = π 10 s