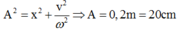Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Va chạm là va chạm mềm nên tại vị trí va chạm: v 0 = m v M + m = v 3 = 2 m / s
Vị trí cân bằng mới của con lắc cách vị trí cân bằng cũ 1 đoạn
OO' = m g k = 0 , 5 . 10 200 = 0 , 025 m = 2 , 5 c m
Ngay sau va chạm con lắc ở vị trí:

Biên độ của con lắc sau va chạm:
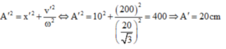

Đáp án C
Khi vật tới biên dưới, vật nhỏ tới va chạm và dính vào nên ta áp dụng bảo toàn động lượng ta có:
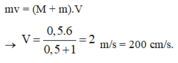
Vị trí cân bằng mới cách vị trí cân bằng cũ 1 đoạn là:
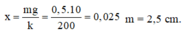
Sau va chạm li độ của vật so với VTCB mới là: x0 = A - x = 10 cm
Biên độ dao động mới của vật là:
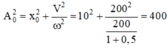
® A0 = 20 cm

Vận tốc của hai vật sau va chạm: (M + m)V = mv
=> V = 0,02\(\sqrt{2}\) (m/s)
Tọa độ ban đầu của hệ hai vật x0 = \(\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}\) = 0,04m = 4cm
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2+\left(M+m\right)}{k}=0,0016\Rightarrow A=0,04m=4cm\)
→ B
Vận tốc của hai vật sau va chạm: \(\left(M+m\right)V=mv\)
\(\rightarrow V=0,02\sqrt{2}\left(m\text{ /}s\right)\)
Tọa độ ban đầu của hệ hai vật: \(x_0=\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}=0,04m=4cm\)
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2\left(M+m\right)}{k}=0,0016\) \(\rightarrow A=0,04m=4cm\)
Đáp án B

Khi vật I qua VTCB thì nó có vận tốc là: \(v=\omega.A\)
Khi thả nhẹ vật II lên trên vật I thì động lượng được bảo toàn
\(\Rightarrow M.v = (M+m)v'\Rightarrow v'=\dfrac{3}{4}v\)
Mà \(v'=\omega'.A'\)
\(\dfrac{v'}{v}=\dfrac{\omega'}{\omega}.\dfrac{A'}{A}=\sqrt{\dfrac{M}{\dfrac{4}{3}M}}.\dfrac{A'}{A}=\dfrac{3}{4}\)
\(\Rightarrow \dfrac{A'}{A}=\dfrac{\sqrt 3}{2}\)
\(\Rightarrow A'=5\sqrt 3cm\)
Chọn A.
Vận tốc của M khi qua VTCB: v = ωA = 10.5 = 50cm/s
Vận tốc của hai vật sau khi m dính vào M: v’ = Mv/(M+v)= 40cm/s
Cơ năng của hệ khi m dính vào M: W = 1/2KA'2= 1/2(m+M)v'2
A’ = 2căn5

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

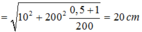
Giải thích: Đáp án B
Phương pháp: Áp dụng định luật bảo toàn động lượng, hê ̣thức độc lập với thời gian của vận tốc và li độ ̣
Cách giải:
Ở vị trí cân bằng lò xo dãn một đoạn ∆l.
Ta có k mg 0,05m 5cm
Khi quả cầu đến vị trí thấp nhất thì lò xo đang dãn đoạn: A + ∆l = 12,5 + 5 = 17,5cm và vận tốc của vật bằng 0.
Sau khi va chạm vận tốc hai vật là: mv = (m+M)v’ => 0,5.6 = 1,5.v’ => v’ = 2m/s.
Sau đó hai vật dao động điều hòa, vị trí cân bằng lò xo dãn ∆l’ với : k ' (m M)g ' 0, 075m 7,5cm
Vậy khi x = 10cm, v’ = 2m/s,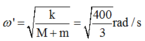
Áp dụng công thức độc lập: