Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hướng dẫn:
+ Trên cạnh thứ nhất lấy hai điểm phân biệt A; B trên cạnh thứ hai lấy hai điểm C; D sao cho khoảng cách từ C; D đến đỉnh của góc lần lượt bằng khoảng cách từ đỉnh của góc với A, B
+ Xác định giao điểm I của BC và AD; tia vẽ từ đỉnh của góc qua I chính là tia phân giác của góc đó.
+ Phần chứng minh tương tự như bài 34
+ Trên cạnh thứ nhất lấy hai điểm phân biệt A; B trên cạnh thứ hai lấy hai điểm C; D sao cho khoảng cách từ C; D đến đỉnh của góc lần lượt bằng khoảng cách từ đỉnh của góc với A, B
+ Xác định giao điểm I của BC và AD; tia vẽ từ đỉnh của góc qua I chính là tia phân giác của góc đó.
+ Phần chứng minh tương tự như bài 34
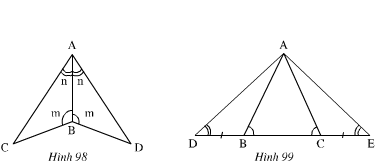
nh 98): Xét ΔABC và ΔABD có:
Nên ΔABC = ΔABD (g.c.g)
- Hình 99): Ta có:
Xét ΔABD và ΔACE có:
Nên ΔABD = ΔACE ( g.c.g)
Xét ΔADC và ΔAEB có:
DC = EB (Vì DC = DB + BC ; EB = EC + BC mà DB = EC)
Nên ΔADC = ΔAEB (g.c.g)
Xem hình 98)
∆ABC và ∆ABD có:
ˆA1A1^=ˆA2A2^(gt)
AB là cạnh chung.
ˆB1B1^=ˆB2B2^(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
ˆB1B1^+ˆB2B2^=1800 (Hai góc kề bù).
ˆC1C1^+ ˆC2C2^=1800 (Hai góc kề bù)
Mà ˆB2B2^=ˆC2C2^(gt)
Nên ˆB1B1^=ˆC1C1^
* ∆ABD và ∆ACE có:
ˆB1B1^=ˆC1C1^(cmt)
BD=EC(gt)
ˆDD^ = ˆEE^(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆDD^=ˆEE^(gt)
ˆC2C2^=ˆB2B2^(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)
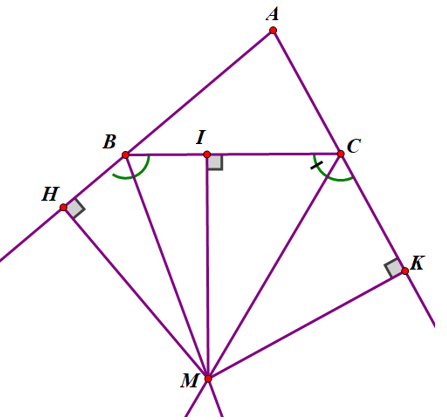
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
(H ∈ tia AB, I ∈ BC, K ∈ tia AC)
Theo định lí 1: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
Dựa vào định lí 2: Điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
⇒ M thuộc phân giác của góc BAC (đpcm).
giúp mình câu 4,6,14 ( sách bài tập toán 7-tập 1) phần hình học chương 1
Bài 6:
A P M N Q 33 o
a) \(\widehat{MAP}=\widehat{NAQ}\) (hai góc đối đỉnh)
Mà \(\widehat{MAP}=33^o\)
Vậy \(\widehat{NAQ}=33^o\).
b) Ta có: \(\widehat{MAP}+\widehat{MAQ}=180^o\) (hai góc kề bù)
Mà \(\widehat{MAP}=33^o\)
Nên \(\widehat{MAQ}=180^o-\widehat{MAP}=180^o-33^o=147^o\)
Vậy \(\widehat{MAQ}=147^o.\)
c) Các cặp góc đối đỉnh:
\(\widehat{MAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAP}\) và \(\widehat{MAQ}\).
d) Các cặp góc bù nhau:
\(\widehat{MAP}\) và \(\widehat{NAP}\)
\(\widehat{NAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAQ}\) và \(\widehat{MAQ}\)
\(\widehat{MAQ}\) và \(\widehat{MAP}\).
Gọi O là đỉnh của góc
⦁ Trên cạnh thứ nhất lấy hai điểm phân biệt A ; B
⦁ Trên cạnh thứ hai lấy hai điểm C ; D sao cho OA = OC, OB = OD
⦁ Xác định giao điểm I của BC và AD ; tia vẽ từ đỉnh O qua I chính là tia phân giác của góc đó.