
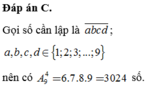
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

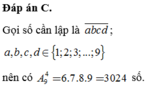

a: \(\overline{abc}\)
a có 5 cách
b có 5 cách
c có 4 cách
=>Có 5*5*4=100 cách
b: \(\overline{abc}\)
a có 2 cách
b có 2 cách
c có 1 cách
=>Có 2*2*1=4 cách
c: \(\overline{abc}\)
a có 3 cách
b có 2 cách
c có 1 cách
=>Có 3*2*1=6 cách

Một số tự nhiên ¯¯¯¯¯¯¯¯¯¯¯¯¯abcdeabcde¯ có 5 chữ số chia hết cho 3 khi tổng các chữ số của nó chia hết cho 3.
Nhận thấy một số tự nhiên thoả yêu cầu sẽ không đồng thời có mặt các chữ số 0 và 3.
Do đó ta chia làm 2 trường hợp:
TH1: ¯¯¯¯¯¯¯¯¯¯¯¯¯abcdeabcde¯ không có chữ số 0.
Khi đó 5 chữ số còn lại có tổng của chúng chia hết cho 3, nên số số tự nhiên thoả mãn là 5! số.
TH2: ¯¯¯¯¯¯¯¯¯¯¯¯¯abcdeabcde¯ không có chữ số 3 (khi đó ta còn 5 chữ số là 0; 1; 2; 4; 5 có tổng của chúng chia hết cho 3).
Suy ra trường hợp này ta có 4.4!4.4! số.
Vậy theo quy tắc cộng ta có tất cả 5!+4.4!=2165!+4.4!=216 số .


Đáp án B.
Sắp xếp 4 số tự nhiên 1, 2, 3, 4 theo thứ tự khác nhau, ta sẽ được một số tự nhiên có 4 chữ số khác nhau. Vậy số cần lập là 4! = 24 (số)


Đáp án A
Tập {1;2;3;4;5;6} có 6 số và tạo thành có 5 vị trí. Mỗi số có 5 chữ số tạo thành một chỉnh hợp chập 5 của 6 chữ số trên
Trong 720 số đó mỗi vị trí (hàng chục nghìn, nghìn, trăm, chục, đơn vị) mỗi chữ số 1, 2, 3, 4, 5, 6 có mặt 720 6 = 120 lần. Tổng các chữ số 1+2+3+4+5+6=21.
Vậy tổng của 720 số tạo thành là 120.21.11111=27999720

Câu 1:
\(\left(x+2\right)f\left(x\right)+x\left(x+1\right)f'\left(x\right)=x\left(x+1\right)\)
\(\Leftrightarrow x\left(x+2\right)f\left(x\right)+x^2\left(x+1\right)f'\left(x\right)=x^2\left(x+1\right)\)
\(\Leftrightarrow\frac{x\left(x+2\right)}{\left(x+1\right)^2}f\left(x\right)+\frac{x^2}{x+1}f'\left(x\right)=\frac{x^2}{x+1}\)
\(\Leftrightarrow\left(\frac{x^2}{x+1}f\left(x\right)\right)'=\frac{x^2}{x+1}=x-1+\frac{1}{x+1}\)
Lấy nguyên hàm 2 vế:
\(\Leftrightarrow\frac{x^2}{x+1}.f\left(x\right)=\frac{x^2}{2}-x+ln\left|x+1\right|+C\)
Thay \(x=1\Rightarrow ln2+\frac{1}{2}=\frac{1}{2}-1+ln2+C\Rightarrow C=1\)
\(\Rightarrow\frac{x^2}{x+1}f\left(x\right)=\frac{x^2}{2}-x+ln\left|x+1\right|+1\)
Thay \(x=2\Rightarrow\frac{4}{3}f\left(2\right)=ln3+1\Rightarrow f\left(2\right)=\frac{3}{4}ln+\frac{3}{4}\Rightarrow T=-\frac{3}{16}\)
Câu 2:
\(I_1=\int\limits^2_0f\left(x\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I_1=x.f\left(x\right)|^2_0-\int\limits^2_0x.f'\left(x\right)dx=2-\int\limits^2_0x.f'\left(x\right)dx\)
Mà \(I_1=2\)\(\Rightarrow I_2=\int\limits^2_0x.f'\left(x\right)dx=-2\)
Đặt \(2x=t\Rightarrow x=\frac{t}{2}\Rightarrow dx=\frac{1}{2}dt\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow t=0\\x=2\Rightarrow t=4\end{matrix}\right.\)
\(\Rightarrow I_2=\int\limits^4_0\frac{t}{2}f'\left(\frac{t}{2}\right).\frac{1}{2}dt=\frac{1}{4}\int\limits^4_0t.f'\left(\frac{t}{2}\right)dt=-2\)
\(\Rightarrow\int\limits^4_0t.f'\left(\frac{t}{2}\right)dt=-8\) hay \(\int\limits^4_0x.f'\left(\frac{x}{2}\right)dx=-8\)