Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Số cách rút hai thẻ chẵn là C 10 2 . Số cách rút ra hai thẻ trong đó có một thẻ ghi số chia hết cho 4 còn thẻ kia ghi số lẻ là .
Vậy xác suất cần tìm là C 5 1 C 5 2
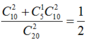

Đáp án A
Chọn 10 tấm bất kỳ có: C 30 10 , trong 30 thẻ có 15 thẻ mang số chẵn, 15 thẻ mang số lẻ và 3 số chia hết cho 10.
Ta chọn 10 tấm thẻ lấy ra 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn, trong đó chỉ có một tấm mang số chia hết cho 10 có: C 15 5 . C 3 1 . C 12 4 cách.
Do đó xác suất cần tìm là: C 15 5 . C 3 1 . C 12 4 C 30 10 = 99 667 .

Đáp án A
Chọn 10 tấm bất kì có C 30 10 , trong 30 thẻ có 15 thẻ mang số chẵn, 15 thẻ mang số lẻ và 3 số chia hết cho 10
Ta chọn 10 tấm thẻ lấy ra có 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn, trong đó chỉ có 1 tấm mang số chia hết cho 10 có: C 15 5 C 3 1 C 12 4 cách
Do đó xác suất cần tìm là C 15 5 C 3 1 C 12 4 C 30 10 = 99 667


Trong 20 tấm thẻ từ 1 đến 20 có 10 tấm thẻ mang số lẻ, 10 tấm thẻ mang số chẵn trong đó có 5 tấm thẻ chia hết cho 5. Gọi A là biến cố: " chọn có 3 tấm thẻ mang số lẻ, 2 tấm thẻ mang số chẵn trong đó có ít nhất một tấm thẻ mang số chia hết cho 4"
TH1: Chọn được 3 tấm thẻ mang số lẻ 1 tấm thẻ mang số chẵn chia hết cho 4 và một tấm chẵn mang số không chia hết cho 4 có: ![]()
TH2: Chọn được 3 tấm thẻ mang số lẻ và 2 tấm thẻ mang số chẵn và chia hết cho 4 có:


Chọn C.
Số phần tử của không gian mẫu là: n Ω = C 11 6 = 462
Gọi A là biến cố “ Chọn ngẫu nhiên 6 tấm thẻ để tổng ghi trên 6 tấm thẻ là một số lẻ”
Các kết quả thuận lợi cho biến cố A.
Lấy ra được 1 tấm thẻ lẻ và 5 tấm thẻ chẵn có C 6 1 . C 5 5
Lấy ra được 3 tấm thẻ lẻ và 3 tấm thẻ chẵn có C 6 3 . C 5 3
Lấy ra được 5 tấm thẻ lẻ và 1 tấm thẻ chẵn có C 6 5 . C 5 1
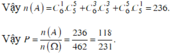

HD: Số phần tử của không gian mẫu là: Ω = C 11 4
Gọi A là biến cố: “Tổng số ghi trên 4 tấm thẻ ấy là một số lẻ”
Khi đó số tấm lẻ được chọn là số lẻ.
Trong 11 số từ 1 đến 11 có 6 số lẻ và 5 số chẵn.

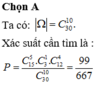



Chọn A.
Lấy ngẫu nhiên tấm thẻ từ 9 tấm thẻ có C 9 2 = 36 cách => số phần tử của không gian mẫu là n Ω = 36 .
Gọi A: “tích của hai số trên tấm thẻ là một số chẵn”.
Để tích của hai số trên tấm thẻ là một số chẵn thì ít nhất một trong hai tấm thẻ phải là số chẵn. Ta có hai trường hợp
TH1: Cả hai thẻ được lấy ra đều là số chẵn có C 4 2 = 6 cách.
Th2: Hai thẻ lấy ra có một thẻ là số chẵn, một thẻ là số lẻ C 4 1 . C 5 1 = 20 cách.
Số kết quả thuận lợi cho A là n(A) = 6 + 20 = 26.
Vậy xác suất của biến cố A là P A = n A n Ω = 13 18 .