Question

[Pham Trong Bach]

Có 15 học sinh giỏi gồm 6 học sinh khối 12, 4 học sinh khối 11 và 5 học sinh khối 10. Hỏi có bao nhiêu cách chọn ra 6 học sinh sao cho mỗi khối có ít nhất 1 học sinh

A. 5005

B. 805

C. 4205

D. 4249

Answer 1

[Cao Minh Tâm]

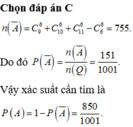
Đáp án C

Phương pháp giải: Sử dụng biến cố đối và các quy tắc đếm cơ bản

Lời giải:

Ta đi làm phần đối của giả thiết, tức là chọn 6 học sinh giỏi chỉ lấy từ một khối hoặc hai khối.

Chọn 6 học sinh giỏi trong 15 học sinh giỏi của 3 khối có C 15 6 = 5005 cách

Số cách chọn 6 học sinh giỏi bằng cách chỉ lấy từ 1 khối 12 là  C 6 6 = 1  

Chọn 6 học sinh giỏi trong 10 học sinh giỏi của 2 khối 12 và 11 có  C 10 6 = 210  cách, tuy nhiên phải trừ đi 1 trường hợp nếu 6 học sinh chỉ ở khối 12 => số cách chọn là 210 – 1 = 2019 cách

Chọn 6 học sinh giỏi trong 11 học sinh giỏi của 2 khối 12 và 10 có  C 11 6 = 462 cách, uy nhiên phải trừ đi 1 trường hợp nếu 6 học sinh chỉ ở khối 12  => số cách chọn là 462 – 1 = 461 cách.

Chọn 6 học sinh giỏi trong 9 học sinh giỏi của 2 khối 11 và 10 có  C 9 6 = 84 cách

Suy ra số cách chọn thỏa mãn yêu cầu bài toán là 5005 – 209 – 461 – 84 – 1 = 4250 cách