Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chứng minh tam giác vuông:
Ứng dụng:
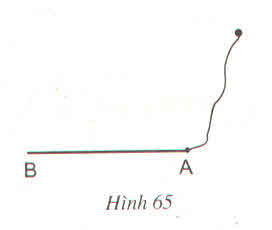
- Vẽ đường tròn (A, r) với r = AB/2; vẽ đường tròn (B, r).
- Gọi C là giao điểm của hai cung tròn nằm ở phía trong tờ giấy.
- Trên tia BC lấy D sao cho BC = CD => AB ⊥ AD.
Thật vậy: ΔABD có AC là trung tuyến ứng với BD (BC = CD) và AC = BC = CD.
=> AC = BD => ∆ABD vuông tại A.

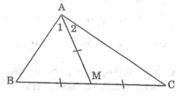
A C B M 1 2
Ta có : MA = MB = MC ( suy từ gt ) .
Các tam giác MAB, MAC cân tại M
Suy ra : \(\widehat{A_1}=\widehat{B}\); \(\widehat{A_2}=\widehat{C}\)( hai góc ở đáy )
Vậy \(\widehat{A_1}+\widehat{A_2}=\widehat{B}+\widehat{C}\)hay \(\widehat{A}=\widehat{B}+\widehat{C}=\frac{180^o}{2}=90^o\)
Vậy \(\Delta ABC\)vuông tại A

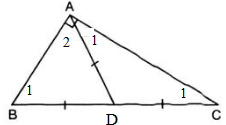
A B C D
Chứng minh :
Giả sử \(\triangle ABC\) có AD là đường trung tuyến ứng với BC và \(DA=\frac{1}{2}BC\).
\(\Rightarrow AD=BD=CD\)
\(+AD=BC\Rightarrow\triangle ADC\text{ cân tại D}\)
\(\Rightarrow\widehat{A_1}=\widehat{C}\)
\(+AD=BD\Rightarrow\triangle ABD\text{ cân tại D}\)
\(\Rightarrow\widehat{A_2}=\widehat{B}\)
\(\Rightarrow\widehat{A_1}+\widehat{A_2}=\widehat{B}+\widehat{C}\)
\(\Rightarrow\widehat{A}=\widehat{B}+\widehat{C}\)
Trong \(\triangle ABC\) có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow\widehat{A}=\widehat{B}+\widehat{C}=\frac{180^0}{2}=90^0\)
hay \(\triangle ABC\) vuông tại A (đpcm)

ΔABE có đường trung tuyến AC bằng 1/2 BE nên ∠(BAE) = 90o.
Vậy AE ⊥ AB.

Giả sử như AM vuông góc với BC
Xét ΔAMB vuông tại M và ΔAMC vuông tại M có
AM chung
MB=MC
Do đó: ΔAMB=ΔAMC
Suy ra: AB=AC(trái với giả thiết)

Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của cạnh BC.
Giả sử AM ⊥ BC. Khi đó AM là đường trung trực của đoạn thẳng BC. Suy ra AB = AC. Điều này mâu thuẫn với giả thiết AB ≠ AC. Vậy trung tuyến AM không vuông góc với BC.

Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của cạnh BC.
Giả sử AM ⊥ BC. Khi đó AM là đường trung trực của đoạn thẳng BC.
Suy ra AB = AC. Điều này mâu thuẫn với giả thiết AB ≠ AC. Vậy trung tuyến AM không vuông góc với BC.
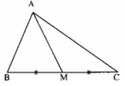
Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của cạnh BC.
Giả sử AM ⊥ BC. Khi đó AM là đường trung trực của đoạn thẳng BC. Suy ra AB = AC. Điều này mâu thuẫn với giả thiết AB ≠ AC. Vậy trung tuyến AM không vuông góc với BC.


Chứng minh tam giác vuông: