Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
+ Khi lực cân bằng trọng lượng, ta có: 3mgcos α - 2mgcos α = mg ⇒ 3 cos α - 2 cos 45 0 = 1
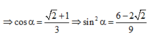
- Gia tốc tiếp tuyến:
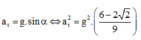
- Gia tốc hướng tâm: 2 g ( cos α - cos α 0 )
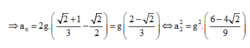
Gia tốc của vật
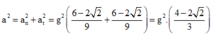
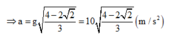

Chọn gốc thế năng tại VT dây thẳng đứng.
Áp dụng định luật bảo toàn năng lượng ta có:
\(W=mgl\left(1-\cos\alpha_0\right)=W_d+W_t=W_d+mgl\left(1-\cos\alpha\right)\)
\(\Rightarrow W_d=mgl\left(1-\cos\alpha_0-1+\cos\alpha\right)=mgl\left(\frac{\alpha^2_0}{2}-\frac{\alpha^2}{2}\right)\)
\(=0,1.10.0,8.\left(\frac{\left(\frac{8}{180}\pi\right)^2-\left(\frac{4}{180}\pi\right)^2}{2}\right)\approx5,84\left(mJ\right)\)

+ \(\omega=\sqrt{\dfrac{g}{l}}=\sqrt{\dfrac{9,8}{0,2}}=7(rad/s)\)
t = 0 vật qua li độ 30 theo chiều dương \(\Rightarrow \varphi = -\dfrac{\pi}{6}\) rad
Vậy PT li độ góc: \(\alpha=6\cos(7t-\dfrac{\pi}{3})(^0)\)
+ Áp dụng: \(v=\sqrt{2gl(\cos\alpha-\cos\alpha_0)}\)
\(\Rightarrow v=\sqrt{2.9,8.0,2(\cos3^0-\cos6^0)}=...\)

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

Chắc là C quá.
Theo mình thì VTCB chỉ có lực căng dây cực đại.Hợp lực cực đại khi chắc là ở biên.
Gia tốc của vật nặng là gia tốc hướng tâm vì nó chuyển động tròn đều nên không hướng về VTCB.

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)
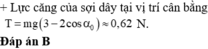
Chọn đáp án C
+ Lực căng dây có độ lớn cực đại khi vật ở vị trí cân bằng:
T max = 3 m g − 2 m g cos α 0 = 2 N
+ Tốc độ của vật khi qua vị trí α = 30 0 là:
v = 2 g l cos α − cos α 0 = 0,856 m/s.
+ Lực căng dây treo khi vật qua vị trí α = 30 0 là:
T = 3mgcos α - 2mgcos α 0 = 1,598 N .
+ Khi qua vị trí cân bằng thì:
v max = 2 g l 1 − cos α 0 = 1 m / s