Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: B.
Gợi ý: Xem lại định nghĩa số thuần ảo, số phức liên hợp và mô đun của số phức.

Giải:
Đặt \(z=a+bi(a,b\in\mathbb{R})\Rightarrow z^2=a^2-b^2+2abi\)
Vì \(z^2\) thuần ảo nên \(a^2-b^2=0\Rightarrow a^2=b^2\)
\(|z|=\sqrt{2}\rightarrow a^2+b^2=2\)
Từ hai điều trên suy ra \(a^2=b^2=1\Rightarrow a=\pm 1,b=\pm 1\)
Vậy tập hợp số phức \(z\) là \(\left \{ \pm 1+i, 1\pm i \right \}\)

Lời giải:
Đặt \(z=a+bi\) với $a,b$ là các số thực.
Ta có: \(|z+2-i|=|(a+2)+i(b-1)|=2\sqrt{2}\)
\(\Leftrightarrow (a+2)^2+(b-1)^2=8(*)\)
Và:
\((z-1)^2=z^2+1-2z=(a+bi)^2+1-2(a+bi)\)
\(=a^2-b^2+2abi+1-2(a+bi)\)
\(=(a^2-b^2+1-2a)+i(2ab-2b)\)
Để \((z-1)^2\) thuần ảo thì \(a^2-b^2+1-2a=0\)
\(\Leftrightarrow (a-1)^2=b^2\)
\(\Leftrightarrow \left[\begin{matrix} a-1=b\\ a-1=-b\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} a=b+1\\ a=1-b\end{matrix}\right.\)
Nếu \(a=b+1\), thay vào (*):
\((b+3)^2+(b-1)^2=8\Leftrightarrow b^2+2b+1=0\Leftrightarrow b=-1\)
\(\Rightarrow a=0\Rightarrow z=-1\)
Nếu \(a=1-b\Rightarrow (3-b)^2+(b-1)^2=8\)
\(\Leftrightarrow b^2-4b+1=0\Rightarrow b=2\pm \sqrt{3}\)
\(\Rightarrow a=-1\mp \sqrt{3}\), tương ứng với 2 số $z$
Vậy có $3$ số thỏa mãn.

\(z=x+y.i\) \(\Rightarrow\overline{z}=x-yi\)
Theo bài ra ta có:
\(\frac{1}{z}=\overline{z}\Leftrightarrow\frac{1}{x+yi}=x-yi\)
\(\Leftrightarrow\left(x+yi\right)\left(x-yi\right)=1\Leftrightarrow x^2+y^2=1\)
\(\Rightarrow\left|z\right|=1\)
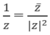
Đáp án: B.
Gợi ý: Xem lại định nghĩa số thuần ảo, số phức liên hợp và mô đun của số phức.