Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(M>\frac{x}{x+y+z+t}+\frac{y}{x+y+z+t}+\frac{z}{x+y+z+t}+\frac{t}{x+y+z+t}=\frac{x+y+z+t}{x+y+z+t}=1\)
Mà \(\frac{a}{b}<1\) thì \(\frac{a}{b}<\frac{a+m}{b+m}\) ; \(m\in N\)*
Do đó \(M<\frac{x+t}{x+y+z+t}+\frac{y+z}{x+y+z+t}+\frac{z+x}{x+y+z+t}+\frac{t+y}{x+y+z+t}=\frac{2\left(x+y+z+t\right)}{x+y+z+t}=2\)
Vậy 1 < M < 2 nên M không phải là số tự nhiên/
Đáp án A
Phương pháp:
Tiếp tuyến của đồ thị hàm số tại M và N song song với nhau 
Cách giải: 
Gọi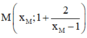 
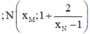là hai điểm thuộc đồ thị hàm số.
Tiếp tuyến của đồ thị hàm số tại M và N song song với nhau
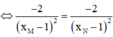
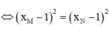
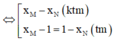
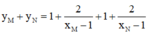
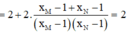
Gọi I là trung điểm của MN ta có: I(1;1)
Dễ thấy đồ thị hàm số có TCN là y = 1 và tiệm cận đứng x = 1 → I(1;1) là giao điểm của hai đường tiệm cận => C đúng.
TCN y = 1 và tiệm cận đứng x = 1 rõ ràng đi qua trung điểm I của đoạn MN=> B, D đúng
làm đc chưa bạn...
gọiE là tđ AD
suy ra NA = NH = NMNM
gọi F là tđ AM thì c/m đc KN KM KA KD bằng nhau
vậy AMN cân vuông tại N
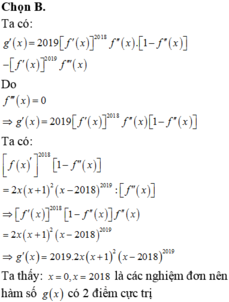
Đáp án D
Các đáp án A, B, C đều đúng, chỉ có D là sai.
Chọn phương án D.