Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Từ giả thiết, suy ra 5 x + 2 y + 1 3 x y - 1 + x + 1 = 5 x y - 1 + 1 3 x + 2 y + x y - 2 y
⇔ 5 x + 2 y - 1 3 x + 2 y + x + 2 y = 5 x y - 1 - 1 3 x y - 1 + ( x y - 1 ) (1)
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 + ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f (t) luôn đồng biến trên ℝ .
Suy ra 1 ⇔ f ( x + 2 y ) = f ( x y - 1 ) ⇔ x + 2 y = x y - 1 ⇔ x + 1 = y ( x - 2 )
y = x + 1 x - 2
Do y > 0 nên x + 1 x - 2 > 0 ⇔ x > 2 x < - 1 . Mà x > 0 nên x > 2.
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm g ' ( x ) = 1 - 3 x - 2 2 > 0 , g ' ( x ) = 0 ⇔ ( x - 2 ) 2 = 3
⇔ x = 2 + 3 ( t m ) x = 2 - 3 ( L ) . Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy m i n g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và y = 1 + 3 .

Toán lớp 0 ????? \(\text{ 🤔 }\text{ 🤔 }\text{ 🤔 }\text{ 😅 }\text{ 😅 }\text{ 😅 }\)

Đáp án C
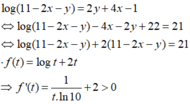
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

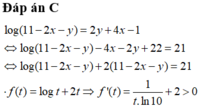
Suy ra f(t) đồng biến trên TXĐ và pt f ( t ) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 - 2 x - y = 10 ⇒ y = 1 - 2 x ⇒ P = 16 x 2 1 - 2 x - 2 x 3 - 6 x + 2 - 1 + 2 x + 5 = - 32 x 3 + 28 x 2 - 8 x + 4 P ' = - 96 x 2 + 56 x - 8 P ' = 0 ⇔ [ x = 1 4 x = 1 3 P 0 = 4 , P 1 3 = 88 27 , P 1 4 = 13 4 , P 1 2 = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

Đáp án D
Phương pháp giải:
Sử dụng phương pháp hàm đặc trưng để từ giả thiết suy ra mối liên hệ giữa hai biến, sau đó sử dụng phương pháp thể và khảo sát hàm số tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức

7/ Em sửa lại đề ạ
Cho hai số thực dương a, b thỏa mãn a+b=4ab
Chứng minh rằng \(\frac{a}{4b^2+1}+\frac{b}{4a^2+1}\ge\frac{1}{2}\)
Đổi biến \(\left(a,b\right)\rightarrow\left(\frac{1}{x},\frac{1}{y}\right)\)
Từ giả thiết => x+y=4
Ta có: BĐT cần CM tương đương với:
\(\frac{\frac{1}{x}}{\frac{4}{y^2}+1}+\frac{\frac{1}{y}}{\frac{4}{x^2}+1}\ge\frac{1}{2}\)\(\Leftrightarrow\frac{y^2}{x\left(4+y^2\right)}+\frac{x^2}{y\left(4+x^2\right)}\ge\frac{1}{2}\left(1\right)\)
Áp dụng BĐT Schwarz, ta có:
∑\(\frac{x^2}{y\left(4+x^2\right)}\ge\frac{\left(x+y\right)^2}{4\left(x+y\right)+xy^2+x^2y}=\frac{16}{16+xy^2+x^2y}\)
Ta chỉ cần chứng minh:
\(xy^2+x^2y\le16\Leftrightarrow xy^2+x^2y\le\frac{1}{4}\left(x+y\right)^3\)
\(\Leftrightarrow xy^2+x^2y\le x^3+y^3\)(luôn đúng)
Do đó (1) đúng. BĐT được chứng minh. Dấu "=" xảy ra khi x=y=2⇔a=b=\(\frac{1}{2}\)
6. (chuyên Hòa Bình)
Cho các số dương x, y, z thỏa mãn: xy+zx+4yz=32
Tìm giá trị nhỏ nhất của\(P=x^2+16y^2+16z^2\)
Áp dụng bất đẳng thức Cauchy cho ba số dương x,y,z ta có
\(\hept{\begin{cases}8y^2+\frac{1}{2}x^2\ge2\sqrt{8y^2.\frac{1}{2}x^2}=4xy\\8z^2+\frac{1}{2}x^2\ge2\sqrt{8z^2.\frac{1}{2}x^2}=4xz\\8y^2+8z^2\ge2\sqrt{8y^2.8z^2}=16yz\end{cases}}\)
Cộng từng vế của ba bđt trên ta có
\(P\ge4\left(xy+xz+4yz\right)=4.32=128\)

Đáp án C
Phương pháp:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Cách giải:
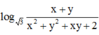
![]()
<=> ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (2)
(2)
Đặt ![]()
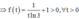
=> f(t) đồng biến trên (0;+∞)
![]()
![]()
<=> ![]()
<=> ![]()
![]()
Khi đó, 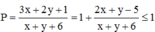
vì 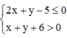
Vậy Pmax = 1 khi và chỉ khi 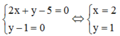

Đáp án C
Phương pháp giải:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Lời giải:
log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y (1)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (2)
(2)
Đặt ![]()
![]()
=> f(t) đồng biến trên (0;+∞)
![]()
![]()
![]()
![]()
![]()
Khi đó, 
vì 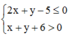
Vậy Pmax = 1 khi và chỉ khi 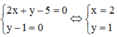
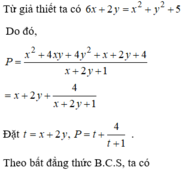
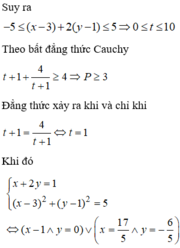
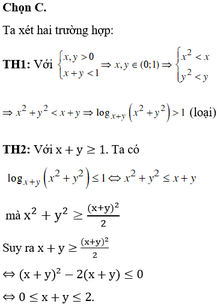
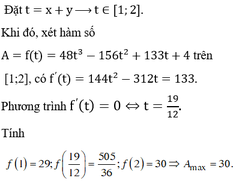
Đáp án C.
Ta có:
G T ⇔ 5 x + 2 y + x + 2 y − 3 − x − 2 y = 5 x y − 1 − 3 1 − x y + x y − 1.
Xét hàm số
f t = 5 t + t − 3 − t ⇒ f t = 5 t ln 5 + 1 + 3 − t ln 3 > 0 ∀ t ∈ ℝ
Do đó hàm số đồng biến trên ℝ suy ra f x + 2 y = f x y − 1 ⇔ x + 2 y = x y − 1
⇔ x = 2 y + 1 y − 1 ⇒ T = 2 y + 1 y − 1 + y . Do x > 0 ⇒ y > 1
Ta có: T = 2 + y + 3 y − 1 = 3 + y − 1 + 3 y − 1 ≥ 3 + 2 3 .