
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

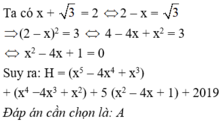

Theo đề ta có
\(x=2-\sqrt{3}\)
\(\Rightarrow\left(4-x\right)x=\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)=1\)
Q = x5 - 3x4 - 3x3 + 6x2 - 20x + 2020
= (x5 - 4x4) + (x4 - 4x3) + (x3 - 4x2) + (10x2 - 40x) + 20x + 2020
= - x3 - x2 - x - 10 + 20x + 2020
= (- x3 + 4x2) + ( - 5x2 + 20x) - x + 2010
= x + 5 - x + 2010 = 2015


\(x+\sqrt{3}=2\Rightarrow\sqrt{3}=2-x\Rightarrow3=\left(2-x\right)^2\Rightarrow x^2-4x+1=0\)
Ta có:
\(B=x^5-4x^4+x^4-4x^3+x^3+5x^2+x^2-20x+5+2013\)
\(\Rightarrow B=x^5-4x^4+x^3+x^4-4x^3+x^2+5x^2-20x+5+2013\)
\(\Rightarrow B=x^3\left(x^2-4x+1\right)+x^2\left(x^2-4x+1\right)+5\left(x^2-4x+1\right)+2013\)
\(\Rightarrow B=x^3.0+x^2.0+5.0+2013=2013\)

b)\(9\left(x-2\right)^2-4\left(x-1\right)^2=\left(9x^2-36x+36\right)-\left(4x^2+8x-4\right)\)
\(=9x^2-36x+36-4x^2+8x-4\)
\(=5x^2-28x+32\)
\(=\left(x-5\right)\left(5x-8\right)\)
\(\hept{\begin{cases}x-5=0\\5x-8=0\end{cases}\Rightarrow}\hept{\begin{cases}x=5\\x=\frac{8}{5}=1\frac{3}{5}\end{cases}}\)
a) \(\left(x+1\right)^2-4\left(x^2-2x+1\right)=0\)
\(\left(x^2+2x+1\right)-\left(4x^2-8x+4\right)=0\)
\(-3x^2+10x-3=0\)
\(\left(3-x\right)\left(3x-1\right)=0\)
\(\hept{\begin{cases}3-x=0\\3x-1=0\end{cases}}\)
\(\hept{\begin{cases}x=3\\x=\frac{1}{3}\end{cases}}\)

6.
Đặt \(\left\{{}\begin{matrix}\sqrt{5x^2+6x+5}=a\\4x=b\end{matrix}\right.\)
\(\Rightarrow a\left(a^2+1\right)=b\left(b^2+1\right)\)
\(\Leftrightarrow a^3-b^3+a-b=0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2+b^2+ab+1\right)=0\)
\(\Leftrightarrow a=b\)
\(\Leftrightarrow\sqrt{5x^2+6x+5}=4x\left(x\ge0\right)\)
\(\Leftrightarrow5x^2+6x+5=16x^2\)
\(\Leftrightarrow11x^2-6x-5=0\)
\(\Rightarrow x=1\)
4. Bạn coi lại đề (chính xác là pt này ko có nghiệm thực)
5.
\(\Leftrightarrow x^2+x+6-\left(2x+1\right)\sqrt{x^2+x+6}+6x-6=0\)
Đặt \(\sqrt{x^2+x+6}=t>0\)
\(t^2-\left(2x+1\right)t+6x-6=0\)
\(\Delta=\left(2x+1\right)^2-4\left(6x-6\right)=\left(2x-5\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}t=\frac{2x+1+2x-5}{2}=2x-2\\t=\frac{2x+1-2x+5}{2}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2+x+6}=2x-2\left(x\ge1\right)\\\sqrt{x^2+x+6}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+x+6=4x^2-8x+4\left(x\ge1\right)\\x^2+x+6=9\end{matrix}\right.\)

\(a,\sqrt{4x^4}+6x^2=2x^2+6x^2=8x^2\)
\(b,\sqrt{25a^4}-2a^2=5a^2-2a^2=3a^2\)
\(c,\sqrt{36a^4}+8a=6a^2+8a\)
\(d,\sqrt{\left(x-3\right)^4}-x^2+3x-1=\left(x-3\right)^2-x^2+3x-1=x^2-6x+9-x^2+3x-1=-3x+8\)

Theo đl Viet: \(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=-3\end{matrix}\right.\)
\(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2=16-\left(-3\right).4=28\)
\(\Rightarrow x_1-x_2=\pm\sqrt{28}=\pm2\sqrt{7}\)
\(\Rightarrow A=\left(x_1-x_2\right)\left(x_1+x_2\right)=\pm2\sqrt{7}.4=\pm8\sqrt{7}\)