

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




1.Xét tam giác OAM và tam giác OBM,ta có:
Cạnh OM là cạnh chung
OA = OB (gt)
góc AOM = góc BOM ( vì Ot là tia phân giác của góc xOy)
=> Tam giác OAM = tam giác OBM (c.g.c)
=> MA = MB ( 2 cạnh tương ứng)
2.Ta có: MA = MB (cmt)
=> Tam giác AMB là tam giác cân
góc MAH = góc MBH ( cmt)
MA = MB ( cmt)
góc AMH = góc BMH ( vì tam giác OAM = tam giác OBM)
=> tam giác AMH và tam giác BMH ( g.c.g)
=> AH = HB ( 2 cạnh tương ứng)
=> H là trung điểm của AB (1)
Vì tam giác AMH = tam giác BMH (cmt)
=>góc MHA = góc MHB ( 2 góc tương ứng)
mà góc MHA + góc MHB = 180 độ ( 2 góc kề bù)
=> góc MHA = góc MHB= 180 độ : 2 = 90 độ
=> MH vuông góc với AB (2)
Từ (1) và (2) => MH là đường trung trực của AB
=> OM là đường trung trực của AB ( vì H thuộc OM )
3.Vì H là trung điểm của AB (cmt)
=> AH =HB = AB : 2 = 6 :2 = 3 (cm)
Xét tam giác OAH vuông tại H
Ta có OA2 =OH2+AH2 (định lý pi ta gô)
\(\Rightarrow\)52=OH2+32
\(\Rightarrow\)25=OH2+9
\(\Rightarrow\)OH2 =25-9
\(\Rightarrow\)OH2=16
\(\Rightarrow\)OH2=\(\sqrt{16}\)
\(\Rightarrow\)OH2=4

Ta có hình vẽ:
O x y t A B M N
a/ Xét tam giác OBM và tam giác OAM có:
OM: chung
MOA = MOB (GT)
OA = OB (GT)
=> tam giác OBM = tam giác OAM (c.g.c)
b/ Ta có: tam giác OAM = tam giác OBM
=> AM = BM (2 cạnh tương ứng)
Ta có: tam giác OAM = tam giác OBM
=> góc OMA = góc OMB (2 góc tương ứng)
Mà góc OMA + góc OMB = 1800
=> góc OMA = góc OMB = 1800:2=900
Vậy OM \(\perp\)AB (đpcm)
c/ Vì OM \(\perp\)AB
và AM = BM
=> OM là trung trực của AB (đpcm)
d/ Xét tam giác ONA và tam giác ONB có:
góc NOA = góc NOB (GT)
ON: cạnh chung
OA = OB (GT)
=> tam giác ONA = tam giác ONB (c.g.c)
=> NA = NB (2 cạnh tương ứng)
a) Xét t/g OBM và t/g OAM có:
OB = OA (gt)
BOM = AOM (gt)
OM là cạnh chung
Do đó, t/g OBM = t/g OAM (c.g.c) (đpcm)
b) t/g OBM = t/g OAM (câu a)
=>BM = AM (2 cạnh tương ứng) (1)
OMB = OMA (2 góc tương ứng)
Mà OMB + OMA = 180o ( kề bù)
Nên OMB = OMA = 90o
=> OM _|_ AB (2)
(1) và (2) là đpcm
c) Có: AM = BM (câu b)
Mà OM _|_ AB (câu b) => OM là đường trung trực của AB (đpcm)
d) C/m tương tự câu a ta cũng có: t/g AON = t/g BON (c.g.c)
=> NA = NB (2 cạnh tương ứng) (đpcm)

Xét tam giác AOC và tam giác BOC có:
AO = BO (gt)
AOC = BOC (OC là tia phân giác của AOB)
OC là cạnh chung
=> Tam giác AOC = Tam giác BOC (c.g.c)
OA = OB (gt)
=> Tam giác OAB cân tại O
mà OI là tia phân giác của AOB
=> OI là đường trung trực của tam giác OAB
=> I là trung điểm của AB
OI _I_ AB
Ta có hình vẽ:
x O y z A B C I
Vì Oz là phân giác của xOy nên \(xOz=zOy=\frac{xOy}{2}\)
Xét Δ AOC và Δ BOC có:
OA = OB (gt)
góc AOC = góc BOC (chứng minh trên)
OC là cạnh chung
Do đó, Δ AOC = Δ BOC (c.g.c) (đpcm)
Vì Δ AOC = Δ BOC nên AC = BC (2 cạnh tương ứng)
góc ACO = góc BCO (2 góc tương ứng)
Xét Δ AIC và Δ BIC có:
AC = BC (chứng minh trên)
góc ACI = BCI (chứng minh trên)
CI là cạnh chung
Do đó, Δ AIC = Δ BIC (c.g.c)
=> AI = IB (2 cạnh tương ứng)
=> I là trung điểm của đoạn AB (đpcm)
Vì Δ AIC = Δ BIC nên góc AIC = BIC (2 góc tương ứng)
Lại có: AIC + BIC = 180o (kề bù)
Do đó, góc AIC = góc BIC = 90o
=> \(AB\perp OC\left(đpcm\right)\)

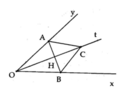
O x y t H A B C
a) Xét2 \(\Delta vuông\)AHO va BHO co
góc AOH = góc BOH ( Ot là tia phân giác góc xOy)
OH là cạnh chung
\(\Rightarrow\Delta AHO=\Delta BHO\)(góc vuông,góc nhọn kề cạnh ấy)
\(\Rightarrow OA=OB\)(2 cạnh tương ứng)
b) Xét \(\Delta OAC\)và \(\Delta OBC\)có:;
OA = OB ( chứng minh trên)
góc AOH = góc BOH ( giả thiết )
OC là cạnh chung
\(\Rightarrow\Delta OAC=\Delta OBC\)(c.g.c)
\(\Rightarrow CA=CB\)( 2 cạnh tương ứng)
và góc OAC = góc OBC ( 2 góc tương ứng)