Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=180^0\)
Do đó: OBDC là tứ giác nội tiếp
b: Xét ΔEBA và ΔECB có
\(\widehat{E}\) chung
\(\widehat{EAB}=\widehat{EBC}\)
Do đó: ΔEBA\(\sim\)ΔECB
Suy ra: EB/EC=EA/EB
hay \(EB^2=EC\cdot EA\)

Đáp án A
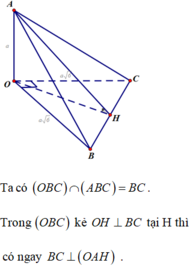
Gọi H là hình chiếu của O lên mặt phẳng (ABC) nên O H ⊥ A B C ⇒ O H ⊥ B C 1 .
Mặt khác O A ⊥ O B , O A ⊥ O C ⇒ O A ⊥ O B C ⇒ O A ⊥ B C 2 .
Từ (1),(2) suy ra B C ⊥ A O H ⇒ B C ⊥ A H . Chứng minh tương tự ta được A B ⊥ C H . Suy ra H là trực tâm của ΔABC.
Trong mặt phẳng (ABC) gọi E là giao điểm của AH và BC.
Ta có O H ⊥ A B C ⇒ O H ⊥ A E tại H.
O A ⊥ A B C ⇒ O A ⊥ O E tức là OH là đường cao của tam giác vuông OAE.
Mặt khác OE là đường cao của tam giác vuông OBC.
Do đó: 1 O H 2 = 1 O A 2 + 1 O E 2 = 1 O A 2 + 1 O B 2 + 1 O C 2 .
⇔ 1 d 2 = 1 a 2 + 1 b 2 + 1 c 2 ⇒ d = a b c b 2 c 2 + a 2 c 2 + a 2 b 2 .

Ta có: \(\widehat{A}=\frac{q}{3}\widehat{C}\).
Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
=> \(\frac{q}{3}\widehat{C}+80^o+\widehat{C}=180^o\)
=> \(\frac{q}{3}\widehat{C}+\widehat{C}=180^o-80^o=100^o\)
=> \(\widehat{C}\left(q+3\right)=300^o\)
=> \(\widehat{C}=\frac{300^o}{q+3}\)
=> \(\widehat{A}=\frac{q}{3}.\frac{300^o}{q+3}=\frac{100^oq}{q+3}\)

Đáp án A
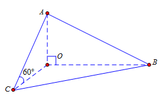
Theo giả thiết OA, OB, OC đôi một vuông góc với nhau nên O A ⊥ O B C , O C là hình chiếu của AC lên mặt phẳng O B C . Do đó, A C O ^ = 60 ° , O A là chiều cao của tứ diện OABC. Xét tam giác vuông AOC có tan 60 ° = O A O C với O A = a ⇒ O C = O A tan 60 ° = a 3 = a 3 3 ; O B = 2 a
Ta có S O B C = 1 2 O B . O C = 1 2 2 a . a 3 3 ; V O A B C = 1 3 O A . S O B C = 1 3 a . a 2 3 3 = a 3 3 9
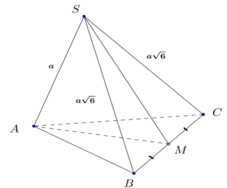
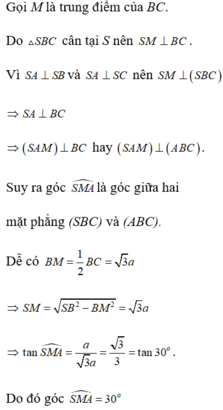
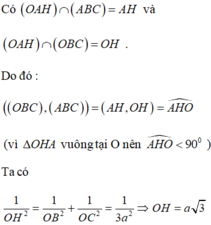

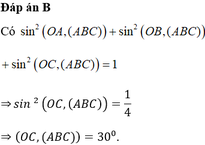
Chọn D