Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A

Phương pháp:
Cách giải:


Mà AH vuông góc (BCD) nên AH là trục của mặt phẳng (BCD).
Gọi K là trung điểm AD, kẻ OK vuông góc với AD, O thuộc AH


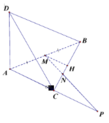
Chọn hệ trục tọa độ Oxyz. Có O = A, AB = Ox, AC = Oy, AD = Oz, AD = 2 α tan 60 o = 2 a 3 , N H = 1 2 - 1 3 B C = 1 6 B C = 1 2 N C
Từ M kẻ MH song song với AC ta có MH = a; CP = 2MH = 2a ⇒ AP = 4a
PT của mặt phẳng (BCD) là x 2 a + y 2 a + z 2 3 a = 1 . Vậy khoảng cách từ P ( 0;4a;0 ) đến (BCD) là:
1 1 4 a 2 + 1 4 a 2 + 1 12 a 2 = a 12 7 = 2 a 21 7
Đáp án cần chọn là A

Đáp án là B

Gọi K là trọng tâm tam giác ABC, N đỗi xứng với D qua J, qua K kẻ KO song song với DN ta có O là tâm mặt cầu cần xác định.
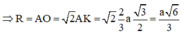


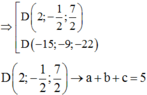

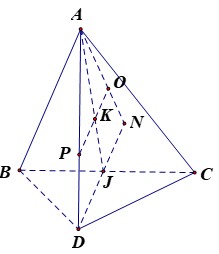
Đáp án là B.
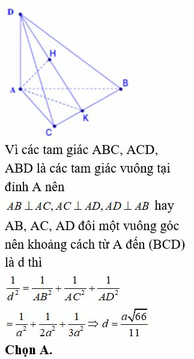
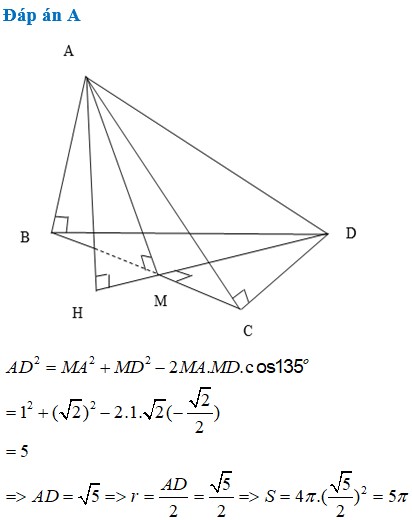
B C = A B 2 = 2 a 2 .Gọi H là trung điểm BC ta có:
A H ⊥ B C B C = A B C ∩ D B C A B C ⊥ D B C ⇒ A H ⊥ D B C
kẻ H E ⊥ D C , H K ⊥ A E (1)
D C ⊥ H E D C ⊥ A H ( d o A H ⊥ D B C ⊂ D C ) ⇒ D C ⊥ A H E ⇒ D C ⊥ H K 2
từ 1 & 2 H K ⊥ A D C ⇒ d H ; A D C = H K
d B ; A D C = 2 d H ; A D C = 2 A H . H E A H 2 + H E 2 = 2 6 3
A H = B C 2 , H E = A B 2 ; A H = B C 2 = a 2 , H E = B C 2 = a