Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Phương pháp:
Cho 
; 
nhận
n
1
→
=
a
1
;
b
1
;
c
1
;
n
2
→
=
a
2
;
b
2
;
c
2
lần lượt là các VTPT. Khi đó, góc giữa hai mặt phẳng
α ; β được tính: cos α ; β = cos n 1 → ; n 2 → = n 1 → . n 2 → n 1 → n 2 →
Với 0 0 ≤ α ≤ 90 0 ⇒ α m i n ⇔ cos α m a x
Cách giải:
(P): x + 2y – 2z +2018 = 0 có 1 VTPT: n 1 → = 1 ; 2 ; - 2
(Q): x + my + (m – 1)z + 2017 = 0 có 1 VTPT: n 2 → = 1 ; m ; m - 1
Góc giữa hai mặt phẳng (P) và (Q):
cos P ; Q = cos n 1 → ; n 2 → = n 1 → . n 2 → n 1 → n 2 →
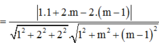
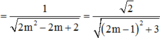
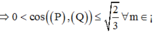
Với 0 0 ≤ α ≤ 90 0 ⇒ α m i n ⇔ cos α m a x
=>((P),(Q))min khi và chỉ khi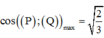 
Khi đó,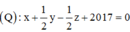 
Ta thấy: 
Thay b + c = a vào ta có :
\(\frac{a}{b}.\frac{a}{c}=\frac{b+c}{b}.\frac{b+c}{c}=\frac{\left(b+c\right)^2}{bc}\) (1)
và \(\frac{a}{b}+\frac{a}{c}=\frac{ac+ab}{bc}=\frac{a.\left(b+c\right)}{bc}=\frac{\left(b+c\right).\left(b+c\right)}{bc}=\frac{\left(b+c\right)^2}{bc}\) (2)
Từ (1) và (2) suy ra \(\frac{a}{b}.\frac{a}{c}=\frac{a}{b}+\frac{a}{c}\)
Có : b+c=a
Thay vào , ta được:
a/b=a/c=> b+c/b.b+c/c=(b+c)2/bc và a/b+a/c=ac+ad/bc=a(b+c)/bc=(bc+c)(b+c)/bc=(b+c)2/bc
Từ trên ta có thể suy ra rằng :
a/b.a/c=a/b+a/c
Bài 3:
Do a và b đều không chia hết cho 3 nhưng khi chia cho 3 thì có cùng số dư nên\(\left[{}\begin{matrix}\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\\\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\end{matrix}\right.\)
TH1:\(\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+1\right)\left(3m+1\right)-1\)
\(\Rightarrow ab-1=9nm+3m+3n+1-1=9nm+3m+3n⋮3\) nên là bội của 3 (đpcm)
TH2:\(\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+2\right)\left(3m+2\right)-1\)
\(\Rightarrow ab-1=9nm+6m+6n+4-1=9nm+6m+6n+3⋮3\) nên là bội của 3 (đpcm)
Vậy ....
Bài 2:
\(B=\frac{1}{2010.2009}-\frac{1}{2009.2008}-\frac{1}{2008.2007}-...-\frac{1}{3.2}-\frac{1}{2.1}\)
\(\Rightarrow B=\frac{1}{2010.2009}-\left(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\right)\)
Đặt A=\(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\)
\(\Rightarrow A=\frac{2009-2008}{2009.2008}+\frac{2008-2007}{2008.2007}+...+\frac{3-2}{3.2}+\frac{2-1}{2.1}\)
\(\Rightarrow A=\frac{2-1}{2.1}+\frac{3-2}{3.2}+...+\frac{2008-2007}{2008.2007}+\frac{2009-2008}{2009.2008}\)
\(\Rightarrow A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{2007}-\frac{1}{2008}+\frac{1}{2008}-\frac{1}{2009}\)
\(\Rightarrow A=1-\frac{1}{2009}\)
\(\Rightarrow B=\frac{1}{2010.2009}-A=\frac{1}{2010.2009}-\left(1-\frac{1}{2009}\right)\)
\(\Rightarrow B=\frac{1}{2010.2009}+\frac{1}{2009}-1=\frac{2011}{2010.2009}-1\)
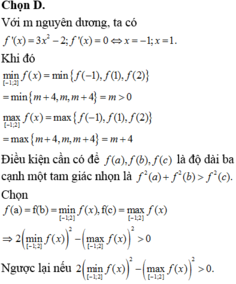
Đáp án D.
Xét khai triển x + y 2018 = C 2018 0 x 2018 + C 2018 1 x 2017 + C 2018 2 x 2016 y 2 + ... + C 2018 2018 y 2018
Chọn x = 3, y = 2 ta có:
5 2018 = C 2018 0 3 2018 + C 2018 1 3 2017 2 + C 2018 2 3 2016 2 2 + ... + C 2018 2018 2 2018 = M
Vậy số chữ số của M = 5 2018 là log M + 1 = log 5 2018 + 1 = 2018. log 5 + 1
Nhập vào màn hình Int 2018 × log 5 + 1 :
Máy hiện kết quả bằng 1411.