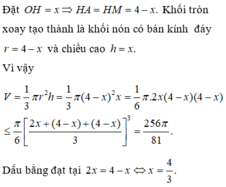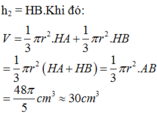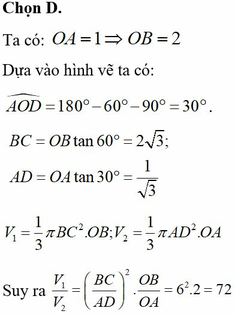Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
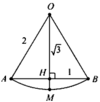
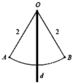
Gọi H, M lần lượt là giao điểm của d với AB và dây cung A B ⏜
Tam giác O A B đều cạnh 2 ⇒ O H = O A 3 2 = 3 ⇒ H M = 2 − 3
Quay tam giác O A B quanh trục d ta được khối nón N có bán kính đáy r = A H = 1 và chiều cao h = O H = 3
⇒ Thể tích khối nón N là V N = 1 3 π r 2 h = 3 3 π
Quay phần hình còn lại quanh trục d ta được chỏm cầu C có bán kính đáy r = A H = 1 và chiều cao h = H M = 2 − 3
⇒ Thể tích khối nón C là V C = π h 6 3 r 2 + h 2 = 16 − 9 3 3 π
Vậy thể tích khối tròn xoay (H) là
V = V N + V C = 16 − 8 3 3 π ≈ 2 , 24
Đáp án B
Giari thích các bước :
Gọi H, M lần lượt là giao điểm của d với AB và dây cung A B ⏜
Tam giác O A B đều cạnh 2 ⇒ O H = O A 3 2 = 3 ⇒ H M = 2 − 3
Quay tam giác O A B quanh trục d ta được khối nón N có bán kính đáy r = A H = 1 và chiều cao h = O H = 3
⇒ Thể tích khối nón N là V N = 1 3 π r 2 h = 3 3 π
Quay phần hình còn lại quanh trục d ta được chỏm cầu C có bán kính đáy r = A H = 1 và chiều cao h = H M = 2 − 3
⇒ Thể tích khối nón C là V C = π h 6 3 r 2 + h 2 = 16 − 9 3 3 π
Vậy thể tích khối tròn xoay (H) là
V = V N + V C = 16 − 8 3 3 π ≈ 2 , 24

Đáp án D
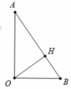
Ta có O A . sin O A H ^ = O H = a ⇒ O A = 2 a
Lại có O B = O A tan A ^ = 2 a 3 suy ra thể tích khối nón tròn xoay tạo bởi tam giác AOB khi quay quanh trục OA là V = 1 3 πOB 2 . OA = 8 9 πa 3

Đáp án B.
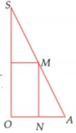
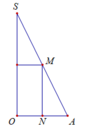
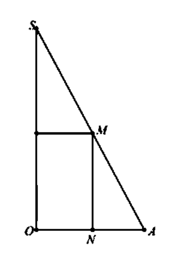
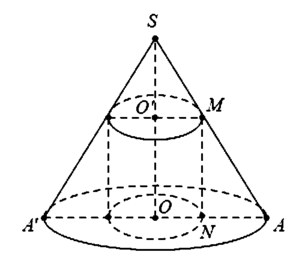
Khi quay hình vẽ quanh trục SO sẽ tạo nên khối trụ nội tiếp hình nón.
Suy ra thiết diện qua trục của hình trụ là hình chữ nhật MNPQ.
Theo định lí Talet, ta có 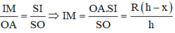
Thể tích khối trụ là 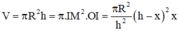
Theo AM – GM ta được
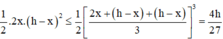
Vậy 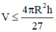 . Dấu “=” xảy ra khi
. Dấu “=” xảy ra khi 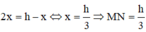

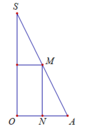
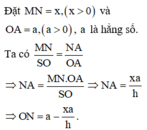
Khối trụ thu được có bán kính đáy bằng ON và chiều cao bằng MN.
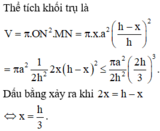
Chọn A

Đáp án B
Đặt SO' = x. Theo định lí Talet ta có:
x
h
=
r
'
r
0
<
x
<
h
Thể tích khối trụ là V = πr ' 2 h - x = π xr 2 h 2 h - x = f x
Ta có f x = πr 2 h 2 x 2 h - x
Cách 1. Xét M x = x 2 h - x
Cách 2. Ta có M x = 4 . x 2 . x 2 . h - x ≤ 4 x 2 + x 2 + h - x 3 3 = 4 h 3 27
Dấu “=” xảy ra ⇔ x 2 = h - x ⇔ x = 2 3 h ⇒ M N = h - x = h 3 .