Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

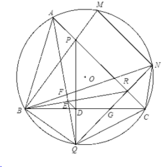
Ta có:
B P Q ^ = B R Q ^ = R B N ^ + R N B ^ = E B F ^ + B A E ^ = 90 0 − B F E ^ + 90 0 − A B E ^ = 180 0 − B F E ^ − A B E ^ = A F B ^ − A B R ^ ⇒ A F B ^ = B P Q ^ + A B R ^

a)Xét tam giác BAD và BED(đều là ta giác vuông)
BD là cạnh chung
ABD=DBE(Vì BD là tia p/giác)
\(\Rightarrow\)tam giác BAD=tam giác BED(cạnh huyền góc nhọn)
\(\Rightarrow\)AB=BE(cặp cạnh tương ứng)
b)Vì tam giác BAD=tam giác BED(cạnh huyền góc nhọn)
\(\Rightarrow\)DA=DE(cặp cạnh tương ứng)
Xét tam giác ADF và EDCđều là ta giác vuông)
DA=DE(CMT)
ADF=EDC(đđ)
\(\Rightarrow\)tam giác ADF=tam giác EDC(cạnh góc vuông góc nhọn)
\(\Rightarrow\)DF=DC(cặp cạnh tương ứng)
Do đó tam giác DFC cân tại D(vì DF=DC)
c)Vì DA=DE(CMT)\(\Rightarrow\)tam giác DAE can tại D
Mà ADE=FDC(đđ)
Mà hai tam giác DAE và CDF cân
Do đó:DAE=DEA=DFC=DCF
\(\Rightarrow\)AE//FC vì DFC=DAE

A B C I M H J K
a. ta có \(BI=\frac{1}{4}BA=\frac{3}{4}\)
Dễ thấy hai tam giác \(\Delta ABM~\Delta CBI\Rightarrow\frac{MB}{IB}=\frac{AB}{BC}\Rightarrow MB=\frac{3}{4}.\frac{3}{4}=\frac{9}{16}\)
vậy \(\frac{BM}{BC}=\frac{9}{64}\).
b.Xét tam giác AJB ta áp dụng địh lý menelaus có
\(\frac{AC}{CJ}.\frac{JK}{KB}.\frac{BI}{IA}=1\Rightarrow\frac{JK}{KB}=\frac{3}{2}\Rightarrow\frac{BK}{KJ}=\frac{2}{3}\)

a) Ta có góc BEC = góc BDC = 90o (góc nội tiếp chắn giữa đường tròn)
Suy ra BD \(\perp\) AC và CE \(\perp\) AB. Mà BD cắt CE tại H là trực tâm \(\Delta\) ABC.
Suy ra AH \(\perp\) BC
Vì AH \(\perp\) BC, BD \(\perp\) AC nên góc HFC = góc HDC = 90o.
Suy ra góc HFC + góc HDC = 180o
Suy ra HFCD là tứ giác nội tiếp
\(\Rightarrow\) góc HDC = góc HCD.
b) Vì M là trung điểm cạnh huyền của hình tam giác vuông ADH nên MD = MA = MH. Tương tự ta có ME = MA = MH
Suy ra MD = ME
Mà OD = OE nên \(\Delta\) OEM = \(\Delta\) ODM \(\Rightarrow\) góc MOE = góc MOD = \(\frac{1}{2}\) góc EOD
Theo qua hệ giữa góc nội tiếp và góc ở tâm cùng chắn cung, ta có góc ECD = \(\frac{1}{2}\) góc EOD
Theo ý a) ta có góc HFD = góc HCD = góc ECD
\(\Rightarrow\) góc MOD = góc HFD hay góc MOD = góc MFD
Suy ra tứ giác MFOD là tứ giác nội tiếp
\(\Rightarrow\) góc MDO = 180o - góc MPO = 90o \(\Rightarrow\) MD \(\perp\) DO
Chứng minh tương tự ta có MEFO là tứ giác nội tiếp
Suy ra 5 điểm M, E, F, O, D cùng thộc 1 đường tròn.

A B C D O M
a) BC vuông góc với AO là theo tính chất hai tiếp tuyến đi qua 1 điểm A
b) Xét hai tam giác DCO và DBA có góc D chung và góc C = góc B = 90 độ (tính chất tiếp tuyến)
=> tam giác DCO đồng dạng với tam giác DBA
=> DC/DB = DO/DA
=> DC.DA = DO.DB (đpcm)
c) Vì OM vuông góc với DB => OM // BA (cùng vuông góc với DB)
Ta có AM/DM + 1 = (AM + DM)/DM = DA/DM
Theo Viet ta có: DA/DM = AB/MO
=> AM/DM + 1 = AB/OM
=> AB/OM - AM/DM = 1 (*)
Ta lại có tam giác MOA cân (vì góc MOA = góc BAO do so le trong, góc MAO = góc BAO do tính chất hai tiếp tuyến cùng 1 điểm)
=> OM = AM
(*) trở thành: AB/AM - AM/DM = 1 (đpcm)

Bài 2:
Giải:
Đổi \(0,6=\frac{3}{5}\)
Tổng độ dài 2 cạnh là:
32 : 2 = 16 ( cm )
Gọi độ dài 2 cạnh của hình chữ nhật là a, b
Ta có: \(\frac{a}{b}=\frac{3}{5}\Rightarrow\frac{a}{3}=\frac{b}{5}\) và a + b = 16
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{a+b}{3+5}=\frac{16}{8}=2\)
+) \(\frac{a}{3}=2\Rightarrow a=6\)
+) \(\frac{b}{5}=2\Rightarrow b=10\)
Vậy chiều dài 2 cạnh của hình chữ nhật là 6 cm; 10 cm
Bài 3:
Ta có: \(y=f\left(x\right)=x2-1\)
Khi \(f\left(x\right)=1\)
\(\Rightarrow1=x2-1\)
\(\Rightarrow2x=2\)
\(\Rightarrow x=1\)
Vậy \(x=1\)
2). Gọi PQ giao BC tại D, AQ giao BR tại E ta có các biến đổi góc sau
E Q D ^ = D Q B ^ − A Q B ^ = P R B ^ − A C B ^ = R B C ^ = E B D ^ .
Vậy tứ giác BEDQ nội tiếp, suy ra B E Q ^ = B D Q ^ = 90 0 ⇒ B R ⊥ A Q