Question

[Đỗ Phạm Nam Hải]

cho tam giác ABC vuông tại A và một điểm D nằm giữa A và B . Đường tròn đường kính BD cắt BC tại E . Các đường thẳng CD , AE lần lượt cắt đường tròn tại F, G . a) cm tam giác ABC đồng dạng với tam giác EBD. b) tứ giác ADEC và AFBC nội tiếp c) AC // FG d) các đường thẳng AC , DE , FB đồng quy
e) D là tâm đường tròn nội tiếp tam giác AEF

*** Giúp mình câu e với , làm ơn

Answer 1

[Nguyễn Ngọc Anh Minh]

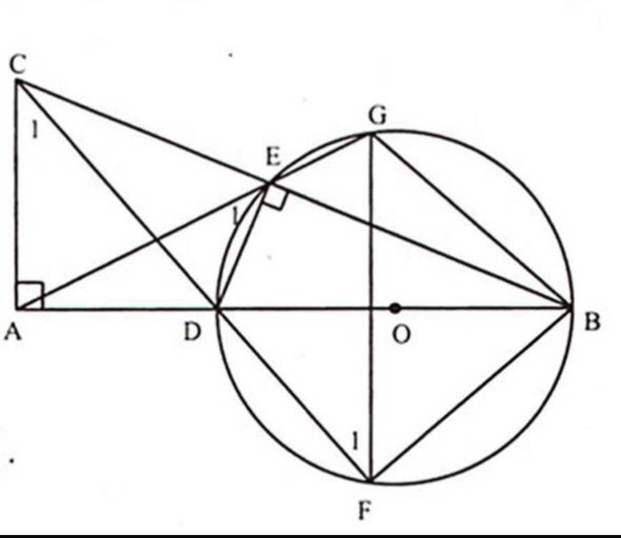
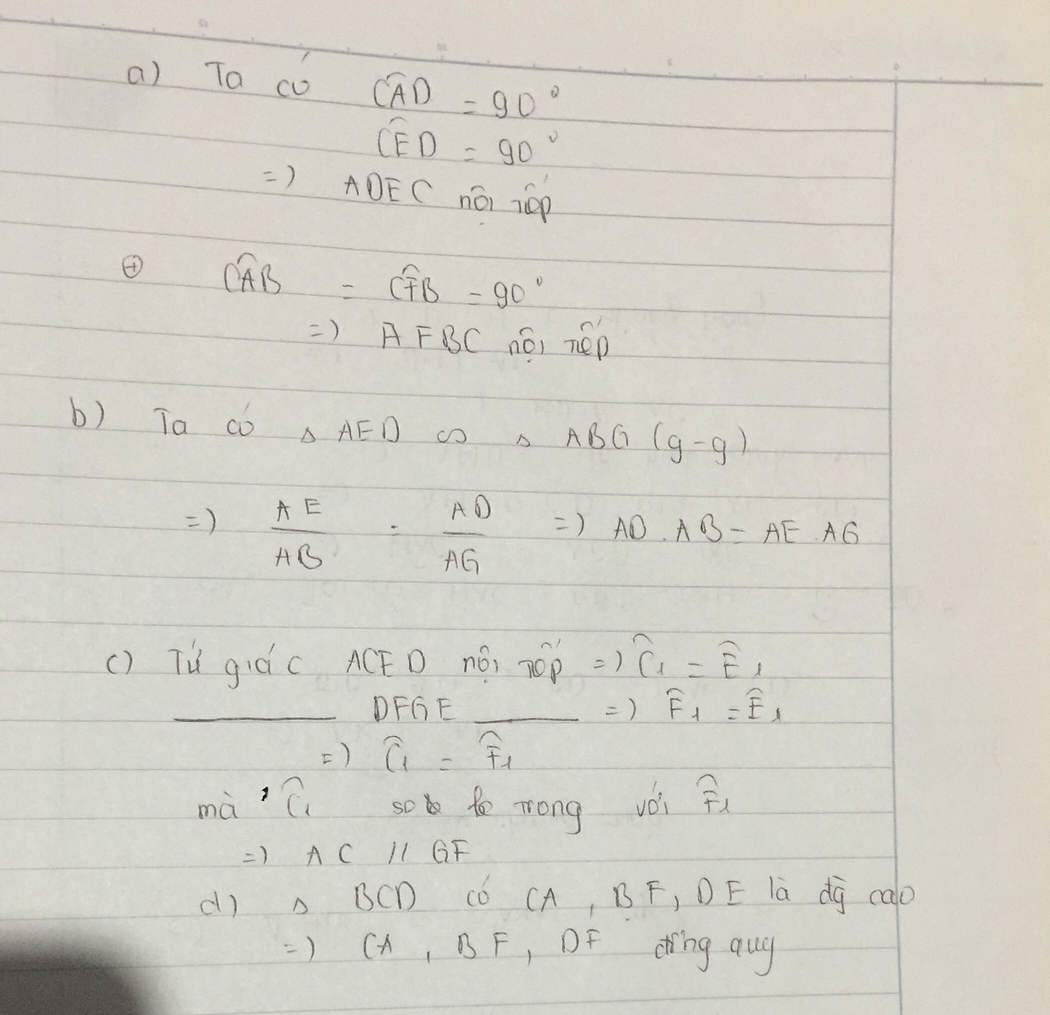
a/

Xét đường tròn đường kính BD

\(\hat{BED}=90^{o}\) (Góc nt chắn nửa đường tròn)

Xét tg vuông ABC và tg vuông EBD

\(\hat{ABC}\) chung

=> △ABC∼△EBD

b/

Ta có A và E cùng nhìn CD dưới 2 góc = nhau và \(=90^{o}\)

=> ADEC là tứ giác nt

Ta có

\(\hat{BFD}=90^{o}\) (Góc nt chắn nửa đường tròn)

=> A và F cùng nhìn BC dưới 2 góc = nhau và \(=90^{o}\)

=> AFBC là tứ giác nt

c/

Xét tứ giác nt ADEC

\(\hat{ACF}=\hat{AED}\) (góc nt cùng chắn cung AD)

Xét tứ giác nt AFBC

\(\hat{ACF}=\hat{ABF}\) (góc nt cùng chắn cung AF)

\(\rArr\hat{AED}=\hat{ABF}\)

Xét đường tròn đường kính BD

\(sđ\hat{AED}=\frac12sđcungDG\) ;\(sđ\hat{ABF}=\frac12sđcungDF\) (Góc nt)

\(\rArr sđcungDG=sđcungDF\)

\(sđ\hat{AED}=\frac12sđcungDF;sđ\hat{CFG}=\frac12sđcungDG\) (góc nt)

\(\rArr\hat{AED}=\hat{CFG}\) mà \(\hat{ACF}=\hat{AED}\) (cmt)

\(\rArr\hat{CFG}=\hat{ACF}\) , 2 góc này ở vị trí so le trong

=> AC//FG

d/

Gọi K là giao của AC với FB

Xét △KBC có

\(\hat{BFD}=90^{o}\) (cmt) => CF⊥KB

\(\hat{BAC}=90^{o}\) (gt) => BA⊥KC

=> D là trực tâm của △KBC

=> KD⊥BC

Mà \(\hat{BED}=90^{o}\) (cmt) => DE⊥BC

=> KD trùng DE (Từ 1 điểm bên ngoài 1 đường thẳng chỉ dựng được duy nhất 1 đường thẳng vuông góc với đường thẳng đã cho)

=> AC; DE; FB đồng quy

e/ Gọi I là giao của FG với AB

Xét đường trong đường kính BD

\(\hat{BGD}=90^{o}\) (Góc nt chắn nửa đường tròn)

Xét tg vuông BFD và tg vuông BGD

\(sđcungDG=sđcungDF\) (cnt) => DF=DG (2 cung có số đo = nhau thì 2 dây trương cung bằng nhau)

BD chung

=> tg BFD = tg BGD (2 tg vuông có cạnh huyền và cạnh góc vuông bằng nhau)

=> BF = BG => △BFG cân tại B

và \(\hat{DBF}=\hat{DBG}\)

=> BD⊥FG và IF = IG (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao và đường trung tuyến)

Xét △AFG có

BD⊥FG (cmt) => AD⊥FG; IF=IG (cmt) => △AFG cân tại A

\(\rArr\hat{DAF}=\hat{DAE}\) (trong tg cân đường cao xuất phát từ đỉnh tg cân đồng thời là đường phân giác) (1)

Xét đường tròn đường kính BD có

\(sđ\hat{FED}=\frac12sddcungDF;sđ\hat{AED}=\frac12sđcungDG\) (góc nt)

Mà \(sđcungDG=sđcungDF\) (cmt)

\(\rArr\hat{FED}=\hat{AED}\) (2)

Xét △AEF

Từ (1) và (2) => D là giao của 3 đường phân giác (trong tg 3 đường phân giác đồng quy)

=> D là tâm đường tròn nội tiếp △AEF