Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

https://alfazi.edu.vn/question/5b8a626cb067113822bfbc62
vào đây để nhận phần quà hấp dẫn nha
và nói là Nick lâm mời nhé
cám ơn và hậu tạ

Ta có : \(\frac{AB}{AC}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\)
Theo định lí Pytago tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow\left(\frac{3}{4}AC\right)^2+AC^2=225\Rightarrow AC=12\)cm
\(\Rightarrow AB=\frac{3}{4}AC=\frac{3}{4}.12=9\)cm
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thúc : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{81}{15}=\frac{27}{5}\)cm
\(\Rightarrow CH=BC-BH=15-\frac{27}{5}=\frac{48}{5}\)cm

Lời giải:
Do $AB:AC=3:4$ nên đặt $AB=3a; AC=4a$ với $a>0$
Áp dụng hệ thức lượng trong tam giác vuông:
$\frac{1}{144}=\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{(3a)^2}+\frac{1}{(4a)^2}=\frac{25}{144a^2}$
$\Rightarrow a^2=25\Rightarrow a=5$ (do $a>0$)
$\Rightarrow AB=3a=15; AC=4a=20$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=9$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=16$ (cm) - theo định lý Pitago

Sử dụng hệ thức về cạnh góc vuông và đường cao trong tam giác vuông, tính được BH =4,5cm, CH = 8cm

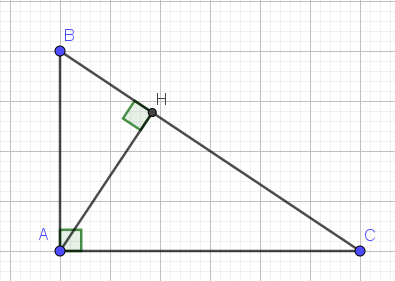
Hình vẽ chung cho cả ba bài.
Bài 1:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{15^2}+\frac{1}{20^2}=\frac{1}{144}\)
\(\Rightarrow AH^2=144\Rightarrow AH=12\)
\(BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=\sqrt{81}=9\)
\(CH=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=\sqrt{256}=16\)
\(\Rightarrow BC=BH+CH=9+16=25\)
Bài 2,3 bạn nhìn hình vẽ và sử dụng hệ thức lượng để tính tiếp như bài 1.
Bài 2: Bài giải
Đặt BH = x (0 < x < 25) (cm) => CH = 25 - x (cm)
Ta có : \(AH^2=BH\cdot CH\text{ }\Rightarrow\text{ }x\left(25-x\right)=144\text{ }\Rightarrow\text{ }x^2-25x+144=0\)
\(\left(x-9\right)\left(x-16\right)=0\text{ }\Rightarrow\orbr{\begin{cases}x=9\\x=16\end{cases}}\left(tm\right)\)
Nếu BH = 9 cm thì CH = 16 cm \(\Rightarrow\text{ }AB=\sqrt{AH^2+BH^2}=\sqrt{9^2+12^2}=15\text{ }\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20\text{ }\left(cm\right)\)
Nếu BH = 16 cm thì CH = 9 cm
\(\Rightarrow\text{ }AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+16^2}=20\text{ }\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{9^2+12^2}=15\text{ }\left(cm\right)\)

Bài 1
a) \(BC=125\Rightarrow BC^2=15625\)
\(\frac{AB}{AC}=\frac{3}{4}\Rightarrow\frac{AB}{3}=\frac{AC}{4}\)từ đây ta có \(\frac{AB^2}{9}=\frac{AC^2}{16}\)
Áp dụng t/c dãy tỉ số bằng nhau ta có
\(\frac{AB^2}{9}=\frac{AC^2}{16}=\frac{AB^2+AC^2}{25}=\frac{BC^2}{25}=\frac{15625}{25}=625\)
\(\frac{AB^2}{9}=625\Rightarrow AB=75\)
\(\frac{AC^2}{16}=625\Rightarrow AC=100\)
Áp dụng hệ thức lượng trong tam giác vuông ta có
\(AB^2=BH\cdot BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{5625}{125}=45\)
\(AC^2=CH\cdot BC\Rightarrow CH=\frac{AC^2}{BC}=\frac{10000}{125}=80\)
b.c) làm tương tự cũng áp dụng HTL trong tam giác vuông
Bài 2
Hình bạn tự vẽ
Ta có \(EH\\ AC\left(EH\perp AB;AC\perp AB\right)\Rightarrow\frac{BE}{AB}=\frac{BH}{BC}\Rightarrow BE=\frac{AB\cdot BH}{BC}\Rightarrow BE^2=\frac{AB^2\cdot BH^2}{BC^2}\)
\(\Leftrightarrow BE^2=\frac{BH\cdot BC\cdot BH^2}{BC^2}=BH^3\)
Bài 3 Đề bài này không đủ dữ kiện tính S của ABC
BH = 50cm, CH = 72cm