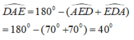
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



ΔABD cân tại B có = 50º nên
= 70º
ΔACE cân tại C có = 50º nên
= 70º

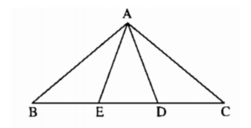
Ta có: \(\Delta\)ABC cân tại A
\(\widehat{A}\) = 100o
=> \(\widehat{B}\) = \(\widehat{C}\) = 20o (Vì tổng các góc trong 1 \(\Delta\) luôn bằng 180o)
* Vì: BA = BD (gt)
=> \(\Delta\)BAD cân tại B.
Ta có: \(\widehat{BAD}+\widehat{B}+B\widehat{DA}=180^O\)
\(\widehat{BAD}+40^{O^{ }}+\widehat{BD}A=180^O\)
\(B\widehat{AD}+\widehat{BDA}=180^{O^{ }}-40^O=120^O\)
Mà \(\Delta\)ABD cân
=> \(\widehat{A}\)= \(\widehat{BDA}\) = 70o
* Vì AC = CE (gt)
=> \(\Delta\)ACE cân tại C.
Ta có: \(\widehat{EAC}+\widehat{C}+\widehat{CEA}=180^O\)
\(\widehat{EAC}+40^O+\widehat{CEA}=180^O\)
\(\widehat{EAC}+\widehat{CEA}=180^O-40^O=140^O\)
Mà \(\Delta\)ACE cân
=> \(\widehat{EAC}=\widehat{CEA}=70^O\)
* Xét \(\Delta\)AED có: \(\widehat{AED}=\widehat{ADE}=70^O\)
Áp dụng định lý tổng các góc trong 1 \(\Delta\) bằng 180o, ta có:
\(\widehat{DAE}+\widehat{ADE}+\widehat{DEA}=180^O\)
\(\widehat{DAE}+70^O+70^O=180^O\)
\(\widehat{DAE}=180^O-70^{O^{ }}-70^O\)
\(\widehat{DAE}=40^O\)
mk tg \(\widehat{B}=\widehat{C}=40\) độ tại 180-100=80 và 80:2=40 ms phải Evil Yasuda

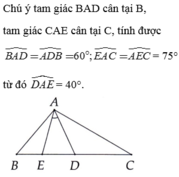
+) Ta có:
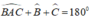 (tổng ba góc trong 1 tam giác)
(tổng ba góc trong 1 tam giác)
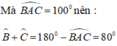
Lại có: tam giác ABC là tam giác cân tại A nên:
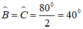
+)Xét tam giác ABD có BA= BD (giả thiết) nên tam giác ABD cân tại B.
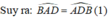
Lại có; 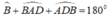 ( tổng ba góc trong 1 tam giác)
( tổng ba góc trong 1 tam giác)
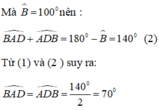
+) Tương tự, ta có tam giác AEC cân tại C ( vì CA =CE)
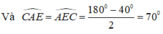
+) Xét tam giác ADE có:
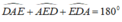 ( tổng ba góc trong tam giác)
( tổng ba góc trong tam giác)
Suy ra: