

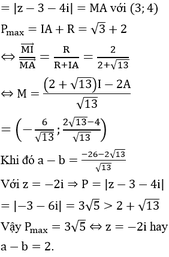
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


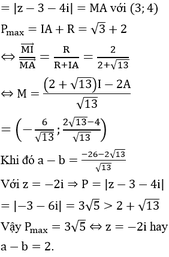

\(x^{15}-\left(7+1\right)x^{14}+\left(7+1\right)x^{13}....+\left(7+1\right)x-5\)
\(=x^{15}-\left(x+1\right)x^{14}+\left(x+1\right)x^{13}....+\left(x+1\right)x-5\)
\(=x^{15}-x^{15}-x^{14}+x^{14}+x^{13}....-x^3-x^2+x^2+x-5\)
\(=x-5=7-5=2\)

ta tính \(y'=6x^2+a-12\)
để hàm số vừa có cực đại và cực tiểu thì \(y'=0\) hai nghiệm phân biệt suy ra \(6x^2+a-12=0\Leftrightarrow6x^2=12-a\) (*)
để (*) có 2 nghiệm phân biệt thì \(12-a>0\Leftrightarrow a<12\)
vậy với a<12 thì hàm số có cực đại và cực tiểu
gọi \(x_1;x_2\) là cực đại và cực tiểu của hàm số
suy ra \(x_{1,2}=\pm\sqrt{\frac{12-a}{6}}\) ta thay vào hàm số suy ra đc \(y_{1,2}\) suy ra \(I\left(x_1;y_1\right);A\left(x_2;y_2\right)\)
sử dụng công thức tính khoảng cách
pt đường thẳng y có dạng x=0
ta có \(d\left(I;y\right)=\frac{\left|x_1\right|}{\sqrt{1}}\); \(d\left(A;y\right)=\frac{\left|x_2\right|}{\sqrt{1}}\)
\(d\left(I,y\right)=d\left(A,y\right)\) giải pt ta tìm ra đc a

Đáp án A.
Gọi M x , y là điểm biểu diễn số phức z.
Từ giả thiết, ta có z − 4 − 3 i = 5 ⇔ x − 4 2 + y − 3 2 = 5 ⇒ M thuộc đường tròn (C) tâm I 4 ; 3 , bán kính R = 5 . Khi đó P = M A + M B , với A − 1 ; 3 , B 1 ; − 1 .
Ta có
P 2 = M A 2 + M B 2 + 2 M A . M B ≤ 2 M A 2 + M B 2 .
Gọi E 0 ; 1 là trung điểm của AB
⇒ M E 2 = M A 2 + M B 2 2 − A B 2 4 .
Do đó P 2 ≤ 4 M E 2 + A B 2 mà
M E ≤ C E = 3 5 s u y r a P 2 ≤ 4. 3 5 2 + 2 5 2 = 200.
Với C là giao điểm của đường thẳng EI
với đường tròn (C).
Vậy P ≤ 10 2 . Dấu “=” xảy ra
⇔ M A = M B M = C ⇒ M 6 ; 4 ⇒ a + b = 10.