Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\left(P\Rightarrow Q\right):\)"Nếu \(x\) là một số hữu tỉ \(x^2\) cũng là một số hữu tỉ". Mệnh đề đúng.
b) Mệnh đề đảo là " Nếu \(x^2\) là một số hữu tỉ thì \(x\) là một số hữu tỉ"
c) Chẳng hạn, với \(x=\sqrt{2}\) mệnh đề này sai

a) \(\left(P\Rightarrow Q\right):\)"Nếu \(x^2=1\) thì \(x=1\)". Mệnh để đảo là "Nếu \(x=1\) thì \(x^2=1\)"
b) Mệnh đề đảo "Nếu \(x=1\) thì \(x^2=1\) là đúng
c) Với \(x=-1\) thì mệnh đề \(\left(P\Rightarrow Q\right):\)sai

a) \(\forall x\in\mathbb{R}:x+\left(-x\right)=0\) (đúng)
Phủ định là \(\exists x\in\mathbb{R}:x+\left(-x\right)\ne0\) (sai)
b) \(\forall x\in\mathbb{R}\)\ \(\left\{0\right\}:x.\dfrac{1}{x}=1\) (đúng
Phủ định là \(\exists x\in\mathbb{R}\)\ \(\left\{0\right\}:x.\dfrac{1}{x}\ne1\) (sai)
c) \(\exists x\in R:x=-x\) (đúng)
Phủ định là \(\forall x\in\mathbb{R}:x\ne-x\) (sai)

a/ \(P:\forall x\in R,x\in Q\Rightarrow2x\in Q\)
\(\overline{P}:\exists x\in R,x\notin Q\Rightarrow2x\notin Q\)
\(\overline{P}\) đúng vì nếu \(\sqrt{2}\notin Q\Rightarrow2\sqrt{2}\notin Q\)
b/ \(\forall x\in R,2x\in Q\Rightarrow x\in Q\)
CM: Vì \(2x\in Q\Rightarrow2x=\frac{m}{n}\left(m,n\in Z;n\ne0\right)\)
\(\Rightarrow x=\frac{1}{2}.\frac{m}{n}\)
Có \(\frac{1}{2}\in Q;\frac{m}{n}\in Q\Rightarrow x\in Q\left(đpcm\right)\)
Phát biểu dưới dạng tương đương: \(\forall x\in R,x\in Q\Leftrightarrow2x\in Q\)

E mới c2 nên cg ch am hiểu lắm nên thôi lm đại nhé:))
Ta có: \(x^2+xy+y^2=\left(x^2+xy+\frac{1}{4}y^2\right)+\frac{3}{4}y^2\)
\(=\left(x+\frac{1}{2}y\right)^2+\frac{3}{4}y^2\ge0\left(\forall x,y\right)\)
Vì nếu \(x=y=0\) => \(x^2+xy+y^2=0\)
=> Mệnh đề sai
Chỉ đúng ở phần không âm
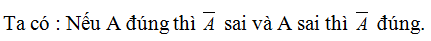
Đáp án A